[Paper Reivew] Class-Imbalanced Semi-Supervised Learning with Adaptive Thresholding
2024. 1. 22. 16:04ㆍPapers/Semi-supervised Learning
Class-Imbalanced Semi-Supervised Learningwith Adaptive Thresholding
Guo, L. Z., & Li, Y. F. (2022, June). Class-imbalanced semi-supervised learning with adaptive thresholding. In International Conference on Machine Learning (pp. 8082-8094). PMLR.
본 논문은 기존의 FixMatch 방법론에서 high fixed confidence threshold의 문제가 있기 때문에 'Adaptive Threshold'이 필요하다고 주장하는 논문이다.
특히, imbalanced semi-supervised (long-tail semi-supervised) 상황에서는 해당 문제가 더욱 부각될 수 있다.
일반적으로 pseudo-label이라는 것 자체가 모델의 예측을 통해서 만들어 내는데, 모델 자체가 편향이 존재한다면, 해당 pseudo-label이 정확하다고 보기 어려울 것이다. 이러한 현상을 흔히 confirmation bias라고 표현하며, 특히 imbalanced problem에서 모델이 majority class에 대해 편향을 가지게되는 것이 일반적이며 이를 confirmation bias라고 논문에서 자주 얘기한다.
따라서 imbalanced 문제에서는 해당 confirmation bias를 줄이는 것을 목표로하는데, 본 논문에서도 제안하는 방식이 confirmation bias가 등장함에도 불구하고 특정 클래스들의 confidence가 낮음을 생각하여 class마다 다른 threshold를 주는 것이 주요한 점이다.

위의 그림에서 6번 식이 의미하는 바는 일반적인 FixMatch에서의 confidence threshold를 보여주며 식 12번은 본 논문에서 제안한 adaptive threshold를 사용하는 것을 의미한다. 빨간색 박스 안의 부분이 바뀐것이 차이점이다. 그렇다면 빨간색 안에 있는 $\tau_{\hat{y}_{b}^{u}}$를 구하는 것이 중요한 내용일 것이다. 그 부분은 이제 아래에서 다루도록 하겠다.
본 논문에서는 Adsh((Ad)aptive Thre(sh)olding)을 이해시키기 위해 두개의 Algorithm을 보여준다.
1번 알고리즘

위의 그림은 전체적인 모델 학습하는 부분을 의미한다.
- 6번줄은 labeled sample에 대한 Supervised cross-entropy loss term이며, FixMatch에서 사용하는 supervised cross-entropy loss term과의 차이가 없다.
- 7번줄부터 11번줄까지의 의미는 unlabeled sample에 대해서 indicator function부분을 제외한 부분인 pseudo-label과 unlabeled sample에 대한 예측값에 대한 cross-entropy 부분이다. 이전 그림에서의 $H(\hat{y}_b^u,f(y|\mathcal{A}(x_b^u);\theta))$부분에 해당하는 연산이다.
- 12번부터 13번줄이 이 논문에서 가장 중요한 'Adaptive Threshold'를 정하는 수식이다. 하지만 $s_k$값을 구하는 식은 알고리즘 2번에서 알 수 있다.
최종적으로 위의 adaptive threshold를 활용하여 15번식에서 사용하고 안하는 sample을 결정하고 평균을 구한 후 16번식에서 최종적으로 두 손실함수의 합을 구한다. 그 후, 17번 식을 통해 최적화를 진행하게 되고, 해당 iteration이 끝나면 $s$를 업데이트 하게 된다.
2번 알고리즘
해당 알고리즘에서는 제일 중요한 $s_k$를 구하는 식을 알 수 있다.

- 2번줄에서 6번줄까지가 모델이 예측한 unlabeled sample에 예측값(확률분포)를 저장하는 리스트를 생성한다. (해당 리스트는 추후 7-17번식에서 활용될 예정)
- 7-14번줄은 $p$를 구하기 위한 연산인데, p는 가장 major class(index=1(코드에서는 0))에 해당하는 위치에서 미리 지정한 $\tau$값보다 낮은 confidence를 가지는 index를 찾고 해당 index 위치를 저장하는 것이 $p$이다. (실제로 X100을 할경우 index문제가 생기기에 실제 코드에서는 100%를 곱해주지 않는다.)
15-17번째줄은 위에서 구한 $p$를 통해서 각 클래스 별로의 $s_k$를 구한다.
이제 위의 $s_k$값을 1번 알고리즘에서의 13번줄에서 활용된다.
위의 알고리즘을 보다 쉽게 이해하기 위해 간단하게 예제 코드를 첨부한다.

각 색깔에 맞는 상자가 코드로 옮겼을때를 의미한다.
결과론적으로 major class의 확률 분포에서 기준이 되는 index위치를 정한 후, 해당 index를 다른 클래스들의 위치를 설정하는데 도움을 준다($p$).
위의 예제의 경우에는 0.94 index 위치가 0.95($\tau$)보다 작기 때문에 해당 인덱스 위치를 0~1사이로 normalize한 값으로 저장하고, 그 위치를 기반으로 다른 클래스들의 위치 또한 찾아낸다.
해당 경우 major class의 경우에는 0.94의 $\tau_1$를 가지며 minor class의 경우에는 0.5(\tau_2)를 가지는 상황이다. 이럴 경우 major class의 경우에는 minor class보다 높은 threshold를 가지게 된다.
Results
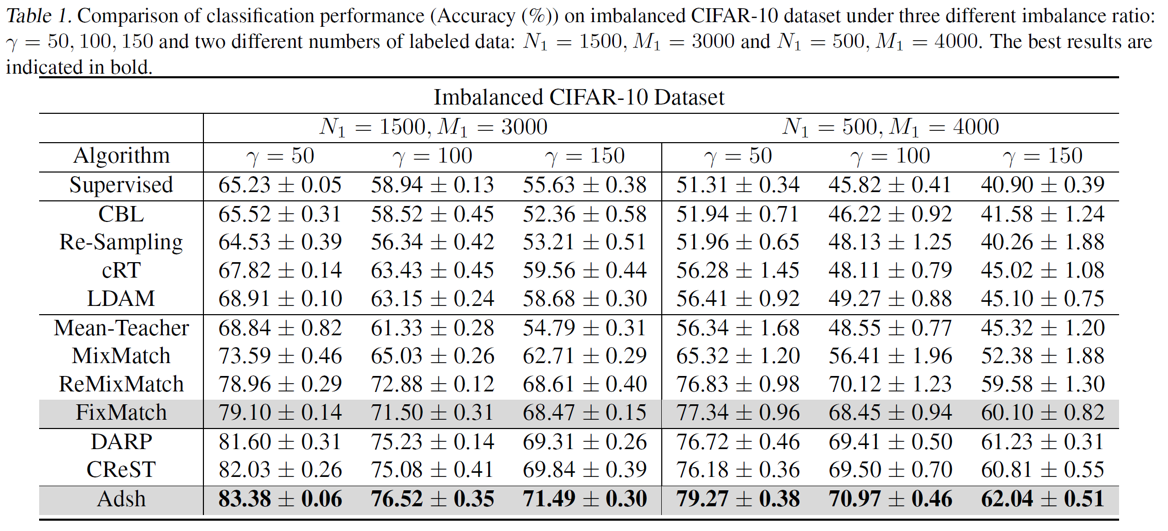

결과론적으로 본 논문에서 방법론이 imbalanced semi-supervised 상황에서 높은 성능을 얻음을 보여준다.
Ablation Study
