[Paper Review] MixMatch : A Holistic Approach to Semi-Supervised Learning
2024. 1. 21. 22:29ㆍPapers/Semi-supervised Learning
MixMatch : A Holistic Approach to Semi-Supervised Learning
Berthelot, D., Carlini, N., Goodfellow, I., Papernot, N., Oliver, A., & Raffel, C. A. (2019). Mixmatch: A holistic approach to semi-supervised learning. Advances in neural information processing systems, 32.
본 논문은 2019년 Nips에 발표된 논문으로, semi-supervised learning에서 'FixMatch'와 마찬가지로 대표적인 논문 중 하나이다. 물론 다음 논문으로 'ReMixMatch'가 있지만, 여전히 많이 backbone 모델로 활용되고 있는 논문이다.
FixMatch와 가장 근본적인 차이는 MixMatch와 ReMixMatch는 Soft pseudo-label 즉, 확률값 자체로 손실함수에서 활용된다. 물론 해당 확률 값을 만들기 위해 몇가지 작업이 존재하지만, 본 리뷰에서 다룰 예정이다.
반대로 FixMatch는 one-hot pseudo-label를 활용하는데, 이는 일반적인 Supervised Learning에서 Cross Entropy를 사용할 때 ground-truth를 one-hot vector로 변환해주는 작업과 동일하기에, 실제로 하나의 index값이 1이고 나머지는 0인 값을 활용하게 된다. 또한 FixMatch에서는 weak augmentation 과 strong augmentation 이 존재하는데, 이는 다음 FixMatch 논문에서 다룰 예정이다.
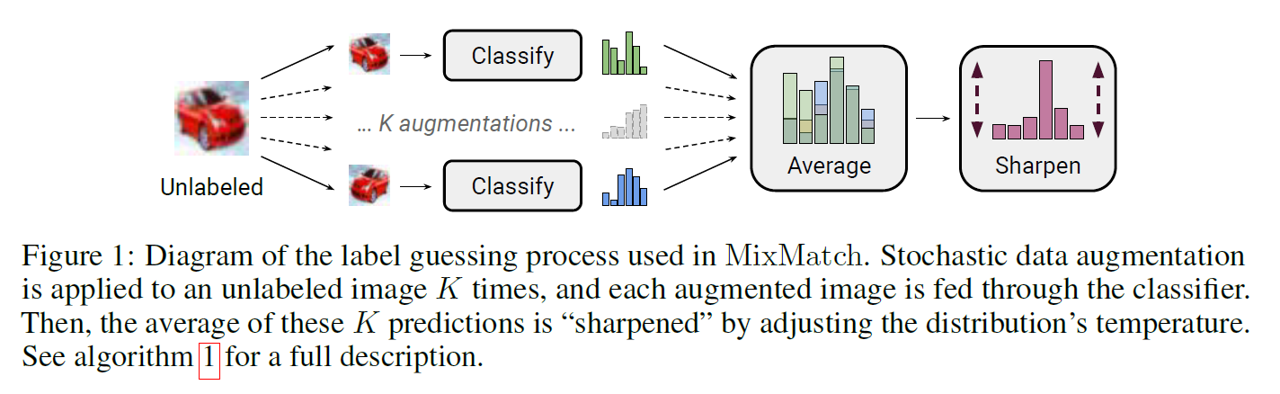
위의 그림은 MixMatch를 보여줄 수 있는 전체적인 요약에 해당되는 그림이다. Unlabeled sample에 대해서 'K'번의 augmentaiton을 수행해서 k개 만큼의 augmented images를 생성한다. 모든 augmented images들의 예측 확률 값 (softmax를 통과한 값)을 구하고, 이를 평균을 통하여 Average 값을 구한다. 최종적으로 pseudo-label을 선택하기 위해 'Sharpen'을 활용하여 가장 높은 확률 값의 크기를 키우고 나머지 영향력을 줄여서 영향력을 조절한다. 결과적으로 Sharpen까지 통과한 값이 Unlabeled sample의 'Pseudo-label'로 활용되고 이를 통해 unlabeled sample을 학습하게 된다.
Related Works
관련 연구에는 본 논문에서는 총 3가지에 대해서 언급한다.
1. Consistency Regularization
2. Entropy Minimization
3. Traditional Regularization
위와 같이 총 3가지에 대해서 얘기한다.
consisntecy regularization은 하나의 이미지에 대해서 augmentation과 noise (다른 모델 weight 또는 dropout과 같이 동일한 입력에 대해서 다른 결과를 만들어내도록 하는 것)을 통하여 얻은 출력 값의 차이를 최소화 하는 것을 목표로 한다. 이전 논문인 Mean Teacher를 읽어보면 쉽게 이해할 수 있기에, 보다 자세히 공부하고 싶다면 해당 논문을 읽어보는 것을 추천한다.
대부분의 Semi-supervised Learning들은 consistecny loss 를 활용하며 같은 방식으로 모델을 학습한다.
Entropy Minimization
MixMatch는 Entropy Minimization을 방영하기 위하여 one-hot vector의 결과르 쓰지 않고 Sharpen 까지 거친 값을 모델 학습에 수행하게 된다. 해당 entropy minimization이 모델 학습 결과를 높일 수 있는가에 대한 답은 안되지만, 일반적으로 'Decision boundary'개념을 생각하게 된다면 어느정도의 margin을 만들 수 있기 때문에 일반화의 효과를 얻을 수 있다고는 할 수 있다. 하지만 일반화의 효과를 얻는다고 꼭 성능이 좋은 것은 아니다. (FixMatch는 one-hot vector만을 씀에도 불구하고 높은 성능을 얻었기 때문이다.)
Traditional Regularization
일반적으로 가장 많이 활용되는 regularization으로 $L_2$ norm을 언급하며, 모델의 가중치의 자유도에 대해서 어느정도 제약을 거는 효과를 통해 regularzation 효과를 볼 수 있는 방법이다. 본 논문에서는 'Mixup'을 통해 해당 효과를 본다. mixup에 대해서는 mixup논문을 읽어보는 것을 추천하며 매우 간단한 원리를 통해 높은 성능을 얻었던 논문이다. (물론 지금은 cutmix나 cutout 등 여러가지 방법론들이 나왔지만, mixup또한 여전히 많이 활용되기에 알아두면 좋다.) 쉽게 말하면, 두 이미지를 overlap 시킨다고 생각하면된다. overlap시킬때 두 비율을 정하는데 비율의 합은 1이고, ground-truth 또한 같은 비율로 overlap시키게 된다.
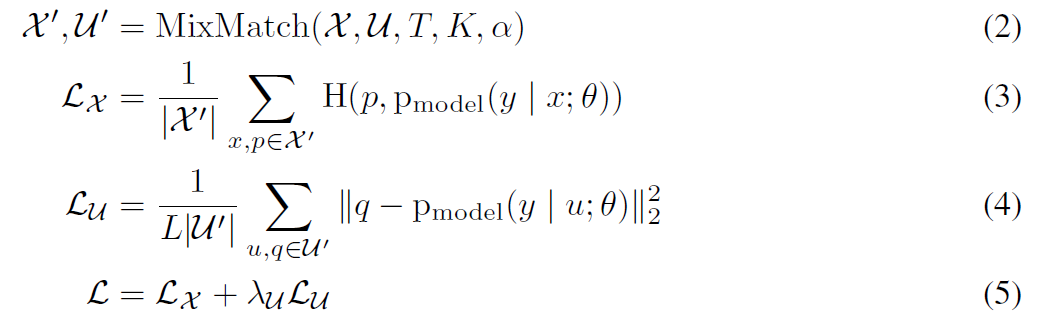
MixMatch를 간단하게 표현하면 위의 식과 나타낼 수 있다. $\mathcal{L}_{\mathcal{X}}$는 일반적으로 labeled sample에 대해서 supervised learning loss 즉 cross-entropy를 사용하게 되는데, MixMatch에서는 labeled sample만 활용해서 3번식을 계산하는게 아닌 Mixup을 통해 만들어진 이미지들이 해당 부분에 들어가게 된다. Mixup은 labeled sample과 unlabeled sample들을 섞게 되는데 보다 자세한건 아래에 algorithm에서 자세히 다루도록 하겠다.
4번 식은 unlabeld sample에 대한 consistency loss를 의미하며, 해당 pseudo-label (q)를 만드는 방법은 위의 식과 마찬가지로 algorith에서 자세히 다루도록하겠다.
최종적으로 5번 식을 통해서 모델을 학습할 때 사용될 손실 함수 값인 $\mathcal{L}$를 구한 후 역전파를 수행하게 된다.

위의 그림은 MixMatch를 수행하기 위해 $\mathcal{X}'$와 $\mathcal{U}'$를 구하기 위한 알고리즘이며, 각각 labeled sample(3)과 unlabeled sample(4번)에 대한 수식에 활용되게 된다.
2번부터 9번수식까지는 맨 처음 그림에서의 'K'번 만큼의 augmentation을 통해 이미지를 만들고 예측을 만드는 과정이다.
labeled sample에 대해서는 한번의 augmentation을 수행하고(3번줄), unlabeled sample에 대해서는 K번 만큼의 augmentation을 통해 증강 후(4-5번줄) 예측의 평균을 구한 후(Average단계,7번줄) Sharpen을 통하여 예측확률을 보다 날카롭게 만들어 주는 과정을 수행한다(8번줄).
그 후, 위에서 언급한 $\mathcal{X}'$와 $\mathcal{U}'$을 만드는 과정을 수행하게 되는데, $\mathcal{W}$는 두 sample의 index를 가지고 있는 집합이며, shuffling을 통해 index를 섞는다. 그 후, 순서대로 labeled sample를 mixup을 통해 생성하고 나머지 index에 대해서는 unlabeled sample과 mixup을 통하여 생성하게 된다.
최종적으로 만들어진 결과들인 $\mathcal{X}'$와 $\mathcal{U}'$을 손실함수 계산하는데 활용하게 된다.
Sharpening

Sharpening은 흔히 temperature softmax라고도 불리며, $T$값을 활용하여 예측 값을 Smoothing하게 하거나 Sharpening하게 만들 수 있다. 일반적으로 1을 기준으로 1보다 클 경우 Smmothing 효과를 볼 수 있으며(예측 분포가 균등해지는 방향으로 변화한다.(T가 크면 클수록)), 반대로 1을 기준으로 작아질 경우에는 Sharpening 효과를 볼 수 있다.
본 논문에서는 Sharpening을 쓰기 위해 T를 0.5로 설정했으며, 원래 예측값보다 좀더 Sharp한 결과를 활용하게 된다.
MixUp
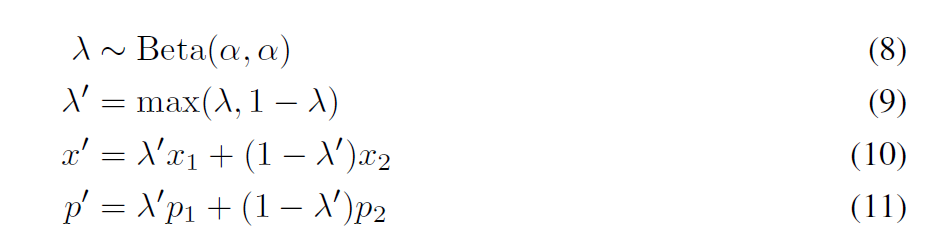
위 알고리즘에서 MixUp을 활용하는 식이 있는데 (13,14번줄) 위의 8-11번식을 활용하여 결과를 만들어 낸다. Beta distribution을 통해 $\lambda$값을 얻어내고, $\lambda$와 $1-\lambda$중 큰 값을 $\lambda'$으로 결정한다. 해당 값을 통해 MixUp을 수행하는데 현재 선택된 $x_1$을 더 많이 활용하고, $x_2$를 적게 활용되는 방향으로 정해진다. 이미지에 대해서 overlap을 수행했으니(10번식), label값도 마찬가지로 overlap을 수행하는 것이 (11번)식이다.
결과
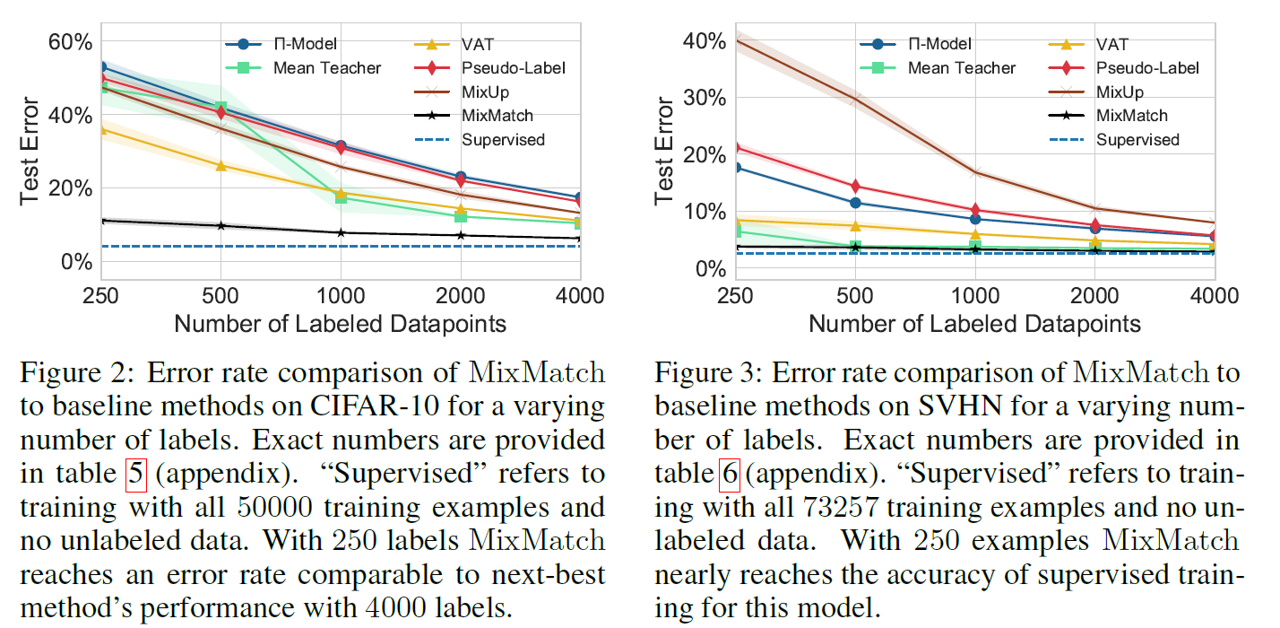
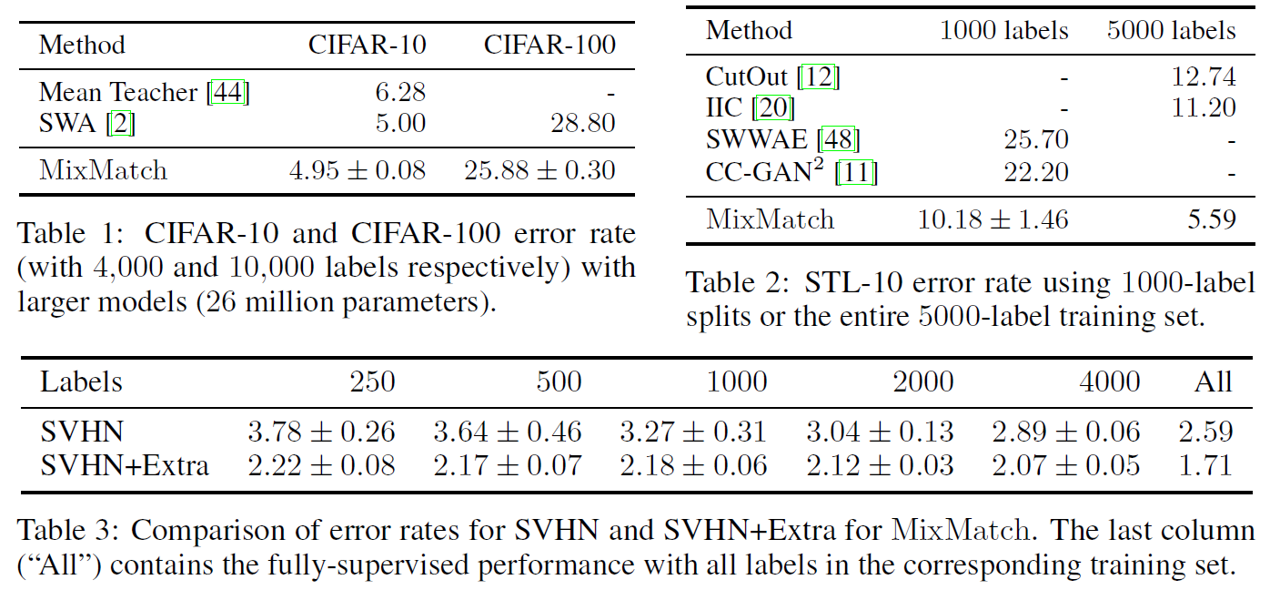
위의 그림과 표는 제안된 논문의 방법론인 MixMatch가 기존의 방법론 보다 높은 성능을 얻었음을 보여주는 결과들이며, 물론 전체 학습 데이터의 label이 있어 모두 labeled sample로 활용 가능한 Supervised 보다는 성능이 낮지만 그에 근사할 만큼의 성능을 얻음을 보여준다. 또한, 다양한 데이터셋에서 CIFAR-10, CIFAR-100, STL-10 그리고 SVHN 데이터셋에서 높은 성능을 얻음을 보여준다.
Ablation Study
