[Paper Review] FreeMatch: Self-Adaptive Thresholding for Semi-Supervised Learning

FreeMatch: Self-Adaptive Thresholding for Semi-Supervised Learning

Wang, Y., Chen, H., Heng, Q., Hou, W., Fan, Y., Wu, Z., ... & Xie, X. (2022). Freematch: Self-adaptive thresholding for semi-supervised learning. arXiv preprint arXiv:2205.07246.

---

요약 : 본 논문은 semi-supervised learning에서 pseudo-label에 대한 confidence를 확인하여 사용할지 안할지를 결정하는 hyper-parameter인 고정된 scalar 값 $\tau$를 adaptive 하게 하여 (global threshold 와 local threshold 두개를 활용함.) semi-supervised learning에서의 높은 성능을 얻고자 한 논문이다. 추가적으로, align loss를 활용하여 보다 높은 성능을 얻고자함.

이전 논문인 'FlexMatch'의 경우에는 고정한 global threshold와 adaptive local threshold를 사용함. 하지만 'FreeMatch'의 경우에는 global threshold 마저 adaptive 하게 하여 uniform distribution semi-supervised learning에서의 성능을 높임.

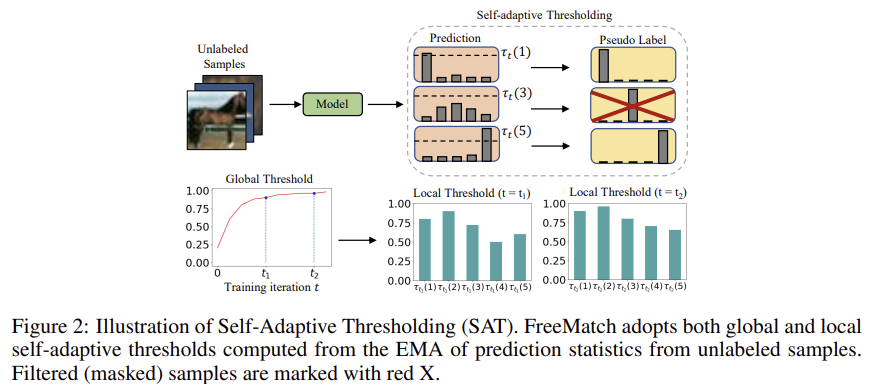
위의 그림은 FreeMatch 논문에서 본 논문을 요약하는 내용이다.

학습이 진행됨에 따라서, Global Threshold는 점진적으로 증가하고 해당 Global Threshold와 Local Threshold 두개의 값을 활용하여 각 클래스별로의 threshold를 정해줄 수 있다. 이를 통하여 기존 고정된 high fixed threshold (0.95)의 값을 썼을 때 생기는 문제인 많은 unlabeled samples들이 학습 반영에 주지 못하는 것을 해결 할 수 있다.

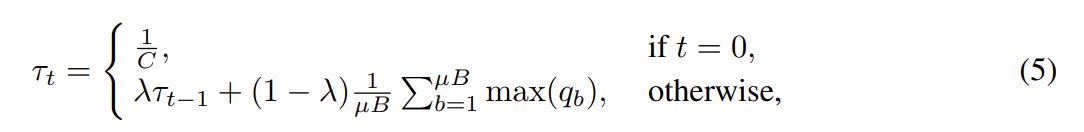
위의 식은 위의 그림에서 언급된것 처럼 Global Threshold를 결정하는 수식이다. 학습 시작일땐 $\frac{1}{C}$를 통해 굉장히 낮은 값으로 시작하고, 학습이 진행됨에 따라 $t\neq{0}$ 일때 진행되는 수식으로 들어가 EMA를 통해 조금씩 update가 진행된다.

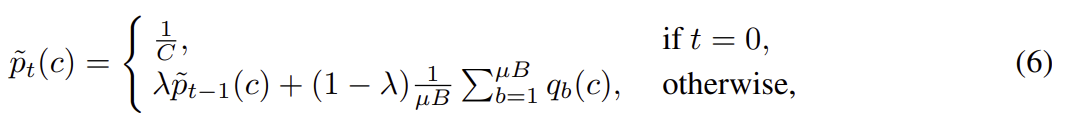
수식 (5)를 통해서 Global Threshold를 구했으니, Local Threshold는 수식 (6)을 통해서 얻을 수 있다. Global Threshold와 마찬가지로 초기화는 $\frac{1}{C}$로 진행하여 균등하게 초기화한 후, 업데이트 또한 마찬가지로 EMA로 업데이트를 진행한다. Global Threshold 와 다른점은 수식 옆에 (c)가 존재하는데, 이는 즉 각 클래스별로의 threshold를 계산하기에 'Local'이란 단어가 붙는 것이다. 이를 업데이트 하기 위하여 현재 mini-batch 안에서의 해당 클래스의 '확률'값을 (one-hot vector 상태에서 처리하는 것이 아닌 예측값 자체 (0~1사이의값))의 평균을 EMA로 업데이트 진행한다.

최종적으로 아래의 수식을 통해서 최종적인 학습에 활용할 Threshold를 정하게 된다.

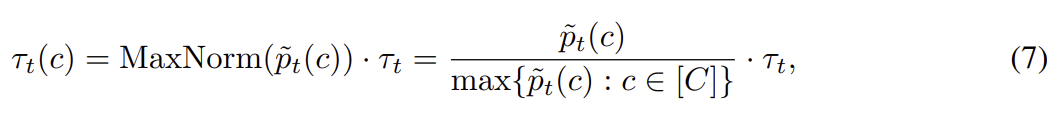
MaxNorm (Maximum Normalization)으로 0~1값으로 변환시킨 후, Global Threshold값을 곱한 값이 해당 클래스의 Local Threshold로 최종적으로 결정되어서 실세 Semi-supervised learning에서 기존의 threshold를 대체하게 된다. 해당 식은 아래와 같다.

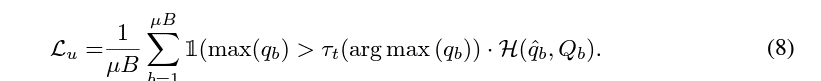
FixMatch에서의 $\tau$ 값의 자리에 $\tau_t(argmax(q_b))$로 대체되고, argmax 함수를 통해 현재 weakly augmented image로부터 예측한 값중 가장 높은 인덱스를 통해 해당 이미지를 무슨 클래스로 선택할건지에 대한 결과를 가져와서 Local Threshold를 선택하게 된다.

Self-Adaptive Fairness

Pseudo-label의 분포가 균형하지 않기 때문에 이를 균형하게 예측하도록 만들기 위해 해당 손실함수를 활용함.

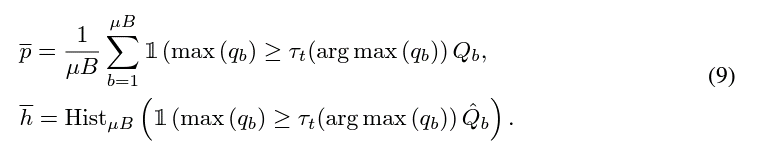
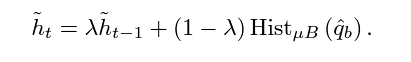
$\bar{p}$ 와 $\bar{h}$ 는 각각 해당 local threshold를 넘는 애들의 현재 미니배치 입력값들의 예측 확률의 평균과 빈도수를 의미한다.

$\tilde{h}$ 와 $\tilede{p}$는 위와 의미들을 EMA로 지속적으로 업데이트가 된 결과이다. 따라서 현재 예측이 굉장히 적은 값이 반영되고 이전까지 누적된 값이 크게 반영되는 형태를 띈다.

최종적으로 위의 Self-Adaptive Fairness 손실함수를 통하여 CrossEntropy의 역수이기 때문에 Maximize를 하는 함수이다. 해당 식에서 Maximize가 되는 상황은 분포 예측값들이 모호한 경우 즉, 균형적으로 예측했을때 손실함수가 가장 최대화가 된다.

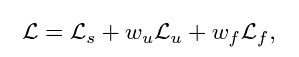
최종적인 손실함수는 위의 9번식과 Self-adaptive Fairness 손실함수의 합이 최종 손실 함수가 된다.

위는 결과이며, 전반적으로 높은 성능을 얻으며 특히 label의 수가 굉장히 적을때 다른 방법론에 비해서 높은 성능을 얻음을 보여준다.