[논문정리] Second-order Attention Network for Single Image Super-Resolution
2020. 1. 3. 11:29ㆍPapers/Super Resolution
Second-order Attention Network for Single Image Super-Resolution
Tao Dai, Jianrui Cai, Yongbing Zhang, Shu-Tao Xia, Lei Zhang; The IEEE Conference on Computer Vision and Pattern Recognition (CVPR), 2019, pp. 11065-11074
해당 논문이 SR 분야에서 대부분의 dataset에서 SOTA를 기록함
Abstract
- 최근 CNNs은 SISR분야(single image super-resolution)에서 널리 사용되며 의미있는 성능을 얻었다.
- 그러나 대부분의 CNN 기반의 SISR 방법들은 주로 넓거나 깊은 구조 디자인에 초점을 맞추었는데 이는 레이어 간의 피처 관계를 탐색하지 않기에 CNNs의 표현력을 방해한다.
- 이 문제를 해결하기 위해서 feature 표현과 feature 관계 학습에 보다 강력한 SAN(second-order attention network)을 제안한다.
- 구제적으로, 보다 판별적 표현을 위한 second-order feature 통계를 사용함으로써 채널별 features를 적응적으로 재조정하기 위해 새로운 학습법인 SOCA(second-order channel attention) 모듈이 개발되었다.
- 더욱이, NLRP(non-locally enhanced residual group)구조를 제안하는데, 이는 비-로컬 연산을 통합하여 장거리 공간 상황 정보를 포착할 뿐만 아니라 보다 feature 표현을 추상적으로 배우기 위한 LSRAG(local-source residual attention groups)을 반복적으로 포함한다.
- SAN은 SISR에서 SOTA를 얻었다.
introduction
- 일반적으로, SISR의 목적은 low-resolution(LR) 입력을 통해 high-resolution(HR)를 생성하는 것이 목적이다.
- SR 방법들은 보간(interpolation)기반, 모델 기반 그리고 최근에는 학습 기반 방법들이 제안되었다.
- 보간 기반 방법들 ( bicubic, bilinear)은 간단하고 효과적이지만 한계가 존재한다.
- 보다 유연한 SR 방법을 위해, 보다 향상된 모델 기반 방법들은 기존의 방법보다는 향상되었지만 여전히 한계가 존재한다.
- CNNs은 다양한 문제에서 많은 성공을 거두었다.
- 이는 SISR에도 유용하게 사용되어졌다.
- 지난 몇년간, CNN 기반의 SISR 방법이 많이 제안되었다.
- CNN은 훈련 데이터 셋에 내재된 이미지 정적을(statics) 활용하여 SISR에서 SOTA를 달성함.
- 비록 SOTA를 달성하였지만 여전히 CNN기반의 SR 방법들은 여전히 몇가지의 한계점들이 존재한다.
- 대부분의 CNN기반의 SR 방법들은 원래의 LR 이미지에서 부터 모든 정보를 사용하지 않기에 상대적으로 낮은 성능을 달성한다.
- 존재하는 대부분의 CNN 기반의 sR 방법들은 깊거나 넓은 네트워크 구조이며 이는 보다 판별적으로 높은-수준의 특징들을 학습하기 위해 초점을 맞추었지만, 중간 레이어에서 드물게 고유의 특징 상관관계를 활용하기 때문에 CNNs의 표현 능력을 방해한다.
- 이를 해결하기 위해서 SAN(second-order attention)을 제안한다.
- 구체적으로 SOCA(second-order channel attention)은 더나은 특징 상관관계를 학습하는 기술이다.
- SOCA는 second-order feature 통계를 first-order대신 활용함으로써 특징 상호 의존성을 학습한다.
- SOCA는 판별 학습 능력을 향상시키고 보다 유익한 특징에 집중한다.
- 더욱이, NLRG(non-locally enhanced residual group) 구조는 장거리 공간 상황 정보를 포착하기 위해 비-로컬 연산을 추가로 통합하기 위해 제공된다.
- LSRAG(local-source residual attention groups) 구조를 쌓음으로써, LR이미지로부터 정보를 활용할 수 있으며 풍부한 low-frequency 정보를 우회를 통하여 허용할 수 있다.
- 아래의 그림을 보면 알 수 있듯이, (h) 논문에서 제안하는 방법은 시각적 질이 보다 좋게 얻었음을 알 수 있고 다른 SOTA SR방법들과 비교하였을때 보다 상세하게 이미지를 복원한다.

- 요약
- 이미지 SR 방법인 SAN을 제안하며 이 방법은 SOTA를 얻었다.
- first-order보다 높은 특징 통계를 고려함으로써 특징을 적응적으로 재조정할 수 있는 SOCA 기술을 제안한다.
- 이러한 SOCA 기술을 통해 네트워크는 보다 유익한 특징에 집중하고 판별적인 학습 능력을 향상시킬 수 있다.
- 또한 네트워크의 학습 속도를 빠르게 하기 위해 공분산 정규화 방법을 반복적으로 활용한다.
- 깊은 네트워크를 만들기위해 NLRG구조를 제안하는데, 이는 공간 상황 정보를 캡처하기 위해 비-로컬 작업을 추가로 통합하고 깊은 특징을 배우기 위해 share-source residual group 사용한다.
Related Work
CNN 기반 SR 방법들
- 최근, CNN기반의 방법들은 SR에서 많이 연구되고 있으며, 그 이유로는 CNN은 비선형 표현력이 강하기 때문이다.
- 대부분에 존재하는 CNN기반의 방법들은 깊거나 넓은 네트워크 구조에 초점을 맞췄다.
- 과거의 방법으로는 세개의 얕은 CNN을 사용한 SRCNN이 있었으며, residual block으로 구성된 16개 이상의 레이어로 만들어진 VDSR과 DRCN이 등장했다.
- 수정된 residual blocks을 쌓아 매우 깊고 넓은 구조로 만든 EDSR이 나왔다.
- dense blocks을 기반으로 만들어진 MemNet과 RDN이 등장했으며 이는 모든 convolutional layers들로부터 모든 계층적 특징들을 활용하는데 초점이 맞춰져있다.
- 추가적으로 네트워크의 깊이를 증가시키는데 초점을 맞추기 위해, NLSR과 RCAN과 같은 몇몇의 다른 네트워크들은 특징 상관 관계를 공간 또는 채널 차원에서 고려함으로써 성능을 향상시켰다.
Attention mechanism
- 인간의 인식에 대한 관심은 일반적으로 인간 시각 시스템이 시각 정보를 적응적으로 처리하고 두드러진 영역에 초점을 맞추는 것을 의미한다.
- 최근 몇가지 시험에서 이미지 및 비디오 분류 작업과 같은 다양한 작업에 대한 CNN의 성능을 향상시키기 위해 주의 처리가 포함되었다.
- 비디오 분류에서 공간 주의를 위한 비-로컬 작업들을 통합시키기 위해 비-로컬 신경망이 제안되었다.
- 반대로, 이미지 분류에서 굉장한 성능을 성취하기 위해 채널-곱 상관 관계를 활용하는 SENet이 제안되었다.
- 최근, SENet은 SR 성능을 보다 향상시킨 깊은 CNNs 소개되었다.
- 그러나, SENet은 오직 first-order 통계(global average pooling)만을 활용하기에 first-order보다 높은 통계를 무시한다. 그렇기 때문에 네트워크의 판별적인 능력을 방해한다.
- 이미지 SR에서,특징에서의 보다 high-frequency 정보는 HR 복원을 위해 굉장히 중요하다.
- 이를 통해, second-order을 활용하는 깊은 SAN(second-order attention network)를 제안한다.
Second-order Attention Network (SAN)

- 위의 그림을 보면 SAN은 주로 4개의 파트로 구분되어있다.
- Shallow feature extraction 얕은 특징 추출
- Non-locally enhanced residual group (NLRG) based deep feature extraction NLRG기반의 깊은 특징 추출
- Upscale module 업스케일
- Reconstruction part 재구축
- 여기서 $I_{LR}$ 과 $I_{SR}$ 은 각각 SAN의 입력과 출력이다.
- $F_0$ = LR 입력으로부터 추출된 얕은 특징
- $F_0 = H_{SF}(I_{LR})$
- $H_{SR}(\cdot)$는 convolution 연산이다. 그 후 추출된 특징인 $F_0$는 NLRG 기반 깊은 특징 추출에 사용되고 이는 다음과 같이 된다.
- $F_{DF} = H_{NLRG}(F_0)$
- 여기서 $H_{NLRG}$는 NLRG 기반의 깊은 특징 추출 모듈이고, 이는 거대한 receptive field를 위한 몇몇의 non-local modules과 $G$ local-source reisudal attention group(LSRAG) 모듈들로 구성되어있다.
- NLRG는 매우 깊은 깊이를 얻으며 그렇기에 매우 큰 receptive fields 크기를 제공한다.
- 그 후 추출된 깊은 특징인 $F_{DF}$는 업스케일 모듈에 사용되며
- $F_{\uparrow} = H_{\uparrow}(F_{DF})$
- 여기서 $H_{\uparrow}$와 $F_{\uparrow}$는 각각 업스케일 모듈과 업스케일된 특징을 뜻한다.
- 마지막 몇 층에 업 스케일링 기능을 포함시키는 방법은 계산 부담과 성능 사이에서 좋은 trade off를 얻을 수 있으므로, 최근 CNN기반 SR 모델에 선호되어지고 있다.
- 업스케일된 특징은 SR 이미지로 만들기 위한 하나의 convolution layer로 매핑된다.
- $I_{SR} = H_R(F_{\uparrow})=H_{SAN}(I_{LR})$
- $H_R(\cdot),F_{\uparrow}$그리고$H_{SAN}$은 각각 재구성 레이어, 업스케일된 특징 그리고 SAN 구조를 의미한다.
- 그후 SAN은 손실 함수에 의해 최적화된다.
- $L_2,L_1$그리고 perceptual 손실 함수들이 널리 사용되어 진다.
- SAN에서는 $L_1$ 손실함수를 사용한다.
- 학습 셋으로 N개의 LR 이미지가 주어지며 그들의 HR 이미지는 $[I_{LR}^i,I_{HR}^i]_{i=1}^N$으로 매칭된다.
- $L(\circleddash) = \frac1N\sum_{i=1}^N{\parallel}H_{SAN}(I_{LR}^i)-I_{HR}^i\parallel_1$
- $\circleddash$는 SAN의 parameter이다.
- 해당 손실 함수는 stochastic gradient descent algorithm으로 최적화된다.
Non-locally Enhanced Residual Group (NLRG)
- NLRG는 몇개의 RL-NL(region-level non-local)과 하나의 SSRG(share-source residual group)구조로 구성되어졌다.
- RL-LR은 풍부한 구조 신호와 HR 자연 장면의 자기 유사성을 활용한다.
- SSRG는 SSC(share-source skip connections)을 가진 LSRAG(local-source residual attention groups)로 구성된다.
- 각 LSRAG에는 SSG로 연결되어 있는 $M$개의 단순화된 residual block과 특징 상호 의존성을 이용하는 second-order channel attention(SOCA)모듈로 구성되어진다.
- 깊은 CNN에서 residual block이 도움이 되는 것은 검증되어졌다.
- 하지만 매우 깊은 네트워크는 기울기 소멸 또는 폭발(gradient vanishing, exploding)에 의해 학습하는데 어려움이나 성능 bottlenect을 제공한다.
- 이를 해결하기 위해 LSRAG를 제안한다.
- 이는 간단하게 레이어를 쌓으면서도 좋은 성능을 얻었다.
- 이를 해결하기 위해서, SSC(share-source skip connection)을 사용하는데 이는 LR 이미지로부터 풍부한 low-frequency를 우회시킴으로써 네트워크 학습 능력을 향상시킨다.
- LSRAG의 $g$번째 그룹은 다음과 같이 나타낼 수 있다.
- $F_g = W_{SSC}F_0+H_g(F_{g-1})$
- $W_{SSC}$는 convolution layer에 사용되는 weight이며 이는 처음에 0으로 초기화된 후 점차적으로 학습하게 된다.
- $H_g(\cdot)$는 $g$번째 LSRAG의 함수이다.
- $F_g,F_{g-1}$는 $g$번째 LSRAG의 입력과 출력이다.
- 깊은 특징은 다음과 같이 얻을 수 있다.
- $F_{DF}=W_{SSC}F_0+F_G$
- 이러한 SSRG구조는 LSRAG를 통한 정보의 흐름을 용이하게 할 뿐만 아니라 고성능의 이미지 SR에 대해 매우 깊은 CNN을 훈련시킬 수 있도록 합니다.
Region-level non-local module (RL-NL)
- 제안된 NLR는 또한 SSRG전후에 연결된 RL-NL 모듈에 의해 LR 기능의 풍부한 구조 신호와 HR 자연 장면의 자기 유사성을 활용한다.
- 비-로컬 신경망은 높은 수준의 작업을 위해 전체 이미지에서 장거리 종속성의 계산을 캡처하기 위해 제안된다.
- 그러나 전통적인 글로번 수준의 비-로컬 작업은 몇가지 이유로 제한될 수 있다.
- 전역 수준의 비-로컬 작업에는 특히 크기가 큰 경우 허용할 수 없는 계산 부담이 필요하다.
- 낮은 수준의 작업(예: SR)에는 적절한 주변 크기의 비-로컬 작업이 선호되어진다.
- 그러므로 더 높은 공간 해상도 또는 성능 저하가 있는 특징인 경우 지역-수준 비-로컬 작업을 수행하는 것이 당연하다.
- 이러한 이유로 지형을 grid로 분할한다. 그런 다음 후속 레이어에 의해 처리된다.
- 비-로컬 작업 후, 특징의 공간적 상관 관계를 활용하여 후속 레어어로 들어가기 전에 특정 표현이 로컬로 향상되지 않는다.
Local-source residual attention group (LSRGA)
- SSC덕분에 풍부한 low-frequency 정보가 후회될 수 있다.
- M개의 간단한 residual blocks을 쌓는다.
- $g$번째 LSRAG의 $m$번째 residual블록은 다음과 같이 표현된다.
- $F_{g,m} = H_{g,m}(F_{g,m-1})$
- $H_{g,m}(\cdot)$은 $g$번째 LSRAG의 $m$번째 reisdual block의 함수를 의미하고 $F_{g,m-1},F_{g,m}$는 입력과 출력을 의미한다.
- 보다 정보적 특징에 초점을 맞추기 위해 local-source skip connect은 출력을 만들기 위해 다음과 같이 하용된다.
- $F_g = W_gF_{g-1}+F_{g,M}$
- $W_g$는 weight이다.
- 이와같은 local-source와 share-source skip connections는 학습하는 동안 풍부한 low-frequency를 우회하도록한다.
- 보다 판별적 표현을 위해 SOCA를 제안한다.
- SOCA는 특징의 second-order 통계를 고려함으로써 채널-곱 특징을 적응적으로 재조정하는 방법을 배운다.
Second-order Channel Attention (SOCA)
- 대부분의 CNN기반의 SR 방법들은 특징의 상호 의존성을 고려하지 않는다.
- SENet은 채널-곱 특징을 재조정하는 것을 소개했었다.
- 그러나 SENet은 오직 first-order 특징의 통계만 전역 평균 풀링을 통해 활용한다. 이는 first-order보다 높은 통계를 무시하며 네트워크의 판별적 기능을 방해한다.
- 다른말로, 최근 작업들은 second-order 통계들이 first-order들보다 보다 판별적 표현에 도움이 되는 것을 보여줬다.
- 위의 관찰에 영감을 받아, second-order 특징 통계를 고려하여 특징 상호 의존성을 배우기 위한 SOCA모듈을 제안한다.
Covariance Normalization
- 기본 feature map $H{\times}W{\times}C$를 $F=[f_1,\cdots,f_c]$인 $H{\times}W$사이즈인 특징맵 $C$로 변환한다.
- $C$차원의 $s=WH$ feature로 feature matrix $X$로 변환시킨다.
- 그 후 공분산 행렬은 다음과 같다.
- $\sum=X\bar{I}X^T$
- $\bar{I}=\frac1s(I-\frac1s1)$에서 $I$는 $s{\times}$ identity 행렬이고 $1$은 1로 구성된 행렬이다.
- 공분산 행렬은 보다 판별적인 표현을 할 수 있도록 해주는 역할을 한다.
- 이러한 이유로, 고유 값 분해 (EIG)를 갖는 획득된 공분산 행렬 $\sum$에 대한 공분산 정규화를 수행한다.
- $\sum = U{\wedge}U^T$
- $U$는 orthogonal 행렬이고 $\wedge = diag(\lambda_1,\cdots,\lambda_c)$는 diagonal 행렬이다.
- 그 후 공분산 정규화는 다음과 같이 전환될 수 있다.
- 공분산 부분은 추후에 공부가 더 정확히 되면 진행하겠습니다.Channel Attention
Channel attention
Covariance Normalization Acceleration
Implementations
- LSRAG는 20개의 SSRG 구조와 2개의 RL-NL 모듈로(맨 앞과 맨 뒤에) 구성되어 있다.
- 각 LSRAG는 10개의 residual blocks과 단일 SOCA모듈을 사용한다.
- SOCA 모듈에서는 축소 비율이 $r=16$인 $1\times1$ convolution 필터를 사용한다.
- SOCA 외부의 다른 convolution 필터의 경우 필터의 크기와 수는 각각 $3\times3$ 및 $C = 64$로 설정된다.
Discussions
Difference to Non-local RNN (NLRN)
- NLRN은 이미지 복원에서 장거리 공간 상황 정보를 캡처하기 위해 비-로컬 작업을 도입함.
- NLRN과 SAN간에는 약간의 차이가 존재
- 먼저, NLRN은 이미지 복원을 위해 RNN에 비-로컬 작업을 포함시키는 반면, SAN은 이미지 SR을 위한 CNN 프레임워크에 비-로컬 작업을 한다.
- 둘째로, NLRN은 각 위치와 그 이웃 사이의 공간적 특징 상관 관계만을 고려하지만, 채널-곱 특징적 상관 관계는 무시한다.
- SAN은 주로 보다 강력한 표현 능력을 위해 특징으 second-order 통계와 채널-곱 기능 상관 관계를 학습하는데 중점을 둔다.
Difference to Residual Dense Network (RDN)
- 기본 블록의 디자인의 차이가 존재한다.
- RDN은 주로 local residual 블록을 학습을 사용하여 고밀로 블록과 로컬 기능 융합을 결합하며 SAN은 기본적인 residual 블록으로 이루어져있다.
- 두번째는 네트워크의 판별적인 능력을 향상시키는 방법이다.
- channel attention는 더 나은 판별적 표현에 효과적인 것으로 나타났다.
- 그러나 RDN은 그러한 정보를 고려하지 않지만 모든 CNN 레이어에서 계층적 기능을 이용하는데 주의를 기울인다.
- 반대로, SAN은 더 나은 판별적 표현을 위해 채널에 관심을 크게 의존한다.
- 따라서 채널-곱 특징 상호 의존성을 효과적으로 학습할 수 있는 SOCA 기술을 제안한다.
Difference to Residual Channel Attention Network (RCAN)
- RCAN은 SAN과 매우 유사하지만 중요 부분에서 차이가 존재한다.
- 첫째, RCAN은 긴 skip connection을 가진 여러개의 residual 블록으로 구성된다.
- SAN은 SSC를 통해 반복 된 residual 그룹을 쌓아서 더 많은 low-frequency 정보를 우회할 수 있습니다.
- 둘째, RCAN은 local receptive fields의 상황 정보만을 이용할 수 있지만 로컬 지역의 외부 정보는 이용할 수 없다.
- SAN은 비-로컬 작업을 통합하여 장거리 공간 상황 정보를 캡처할 뿐만 아니라 receptive fields를 확대함으로써 이 문제를 완화할 수 있다.
- 셋째, RCAN은 네트워크의 판별적 능력을 향상시키기 위해 전역 평균 풀링을 통한 channel attention기반 first-order 통계만을 고려한다.
- SAN은 second-order 특징 통계를 기반으로 channel attention을 학습한다.
- 우리가 아는한, 이미지 SR에 대한 second-order 특징 통계를 기반이 더 효율적이다.
Experiments
Setup
-
학습 데이터셋 : DIV2K
-
벤치마킹 데이터셋 : Set5 , Set14, BSD100, Urban100 그리고 Manga109 (각각의 데이터셋은 다른 특징들을 가지고 있다.)
-
LR로 만들기 위해 bicubic과 blur-downscale을 사용하여 악화시킨다.
-
모든 결과는 PSNR과 SSIM으로 평가된다.
-
학습하는 동안 학습 이미지들은 임의적으로 90,180,270로 회전시키고 수평 뒤집기로 처리한다.
-
각 미니-배치마다 8개의 LR 이미지를 넣으며 크기는 48X48이다.
-
ADAM을 사용하며 $\beta_1=0.9,\beta_2=0.99$그리고 $\varepsilon=10^{-8}$이다.
-
학습률은 $10^{-4}$로 초기화하며 200 epochs마다 반으로 감소시킨다.
Ablation Study
- SAN은 NLRG와 SOCA 두개의 주요 구성을 포함한다.
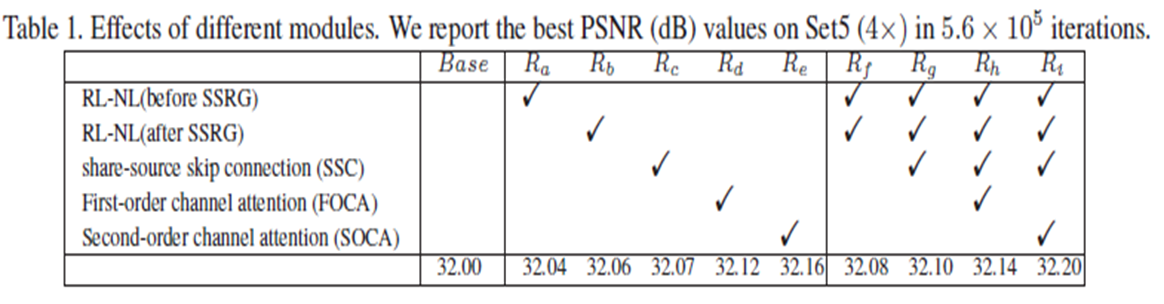
Non-locally Enhance Residual Group (NLRG)
- Base는 각 LSRAG에 20개의 LSRAG 및 10개의 residual 블록을 갖는 CNN만 포함하는 매우 기본적인 베이스라인을 나타내며, 그 결과 400개 이상의 CNN 레이어가 있는 깊은 네트워크가 된다.
- 기본 모델에서 길고 짧은 skip connection을 추가한다.
- Set5(x4)에서 Base가 PSNR = 32.00dB 에 도달함을 알 수 있다.
- $R_a ~ R_e$까지의 결과는 개별 모듈의 효과를 검증한다. 모듈 하나만 사용하면 기본 모델보다 성능이 향상되기 때문이다.
- 특히 얕은 (SSRG 이전) 또는 깊은 계층 (SSRG 이후)에 단일 RL-NL을 추가하는 $R_a,R_b$는 유사한 SR 결과를 얻고 Base를 능가하며 RL-NL의 효과를 검증한다.
- SSC만 추가하면 $R_c$ 성능을 32.00dB에서 32.07dB로 향상시킬 수 있다.
- 주된 이유는 SSC가 LR이미지에서 풍부한 low-frequency 정보를 우회할 수 있기 때문이다.
- $R_a,R_b$를 모두 사용하면($R_f$)성능을 더욱 향상시킬 수 있다.
- RL-NL 모듈이 $R_f$보다 훨씬 나은 성능을 얻을 수 없으므로 성능과 효율의 균형을 맞추기 위해 해당 방법을 사용한다.
Second-order Channel Attention (SOCA)
- 또한 $R_d,R_e,R_h및R_i$의 결과에서 SOCA의 효과를 보여준다.
- 구체적으로, $R_d$는 first-order 특징 통계를 기반으로 전역 평균 풀링을 사용하여 channel attention을 의미한다.
- $R_e$는 second-order 특징 통계를 기반으로하고 이는 SOCA를 이끈다.
- 위의 방법들 모두 좋은 성능을 얻음을 알 수 있다.
- 이는 channel attention이 성능을 결정하는데 중요한 역할을 한다는 것을 나타낸다.
- 또한 FOCA와 비교하여 SOCA는 다른 모듈(예: RL-NL 및 SSC)와 결합하더라도 일관되게 더 나은 결과를 보여준다.
- 이러한 관찰에서 SOCA는 우수성을 보여준다.
Bicubic Degradation (BI)의 결과
- 또한 자체 앙상블 방식을 채택하여 SAN을 강화한다. (SAN+)
- 다른 방법과 비교하여 SAN+는 다양한 스케일링 요소에서 모든 데이터셋에서 최상의 결과를 보여준다.
- 자체 앙상블이 없으면 SAN과 RCAN은 매우 유사한 결과를 얻고 다른 방법들은 능가한다.




- 이는 둘 다 특징 상호 의존성을 배우기 위해 channel attention을 채택하여 네트워크가 보다 유익한 기능에 집중하기 때문이다.
- 텍스쳐는 고차 패턴이며 더 복잡한 통계적 특성을 갖는 반면 테두리는 1차 기울기 연산자로 추출할 수 있는 1차 패턴이다.
- 따라서 second-order 특징 통계를 기반으로하는 SOCA는 더 높은 수준의 정보(예:텍스처)가 있는 이미지에서 더 잘 작동한다.
Blur-downscale Degradation 결과

Model 크기

Conclusions
- 정확한 이미지 SR을 위한 깊은 SAN을 제안한다.
- 특히, LNRG 구조를 통해 SAN은 비-로컬 작업 네트워크에 포함시켜 장거리 종속성 및 구조 정보를 캡처할 수 있다.
- 한편, NLRG는 LR 이미지로부터 풍부한 low-frequency 정보가 SSC를 통해 우회하도록 한다.
- 공간적 특징 상관 관계를 이용하는 것 외에도, 보다 판별적인 표현을 위해 전역 공분산 풀링을 통해 특징적 상호 의존성을 배우는 SOCA 모듈을 제안한다.
- BI 및 BD 저하 모델을 사용한 SR에 대한 광범위한 실험은 정량적 및 시각적 결과 측면에서 SAN의 효과를 보여준다.