2022. 5. 24. 15:17ㆍPapers/Object Detection
MLP-Mixer: An all-MLP Architecture for Vision
Tolstikhin, I. O., Houlsby, N., Kolesnikov, A., Beyer, L., Zhai, X., Unterthiner, T., ... & Dosovitskiy, A. (2021). Mlp-mixer: An all-mlp architecture for vision. Advances in Neural Information Processing Systems, 34.
Main idea in this paper
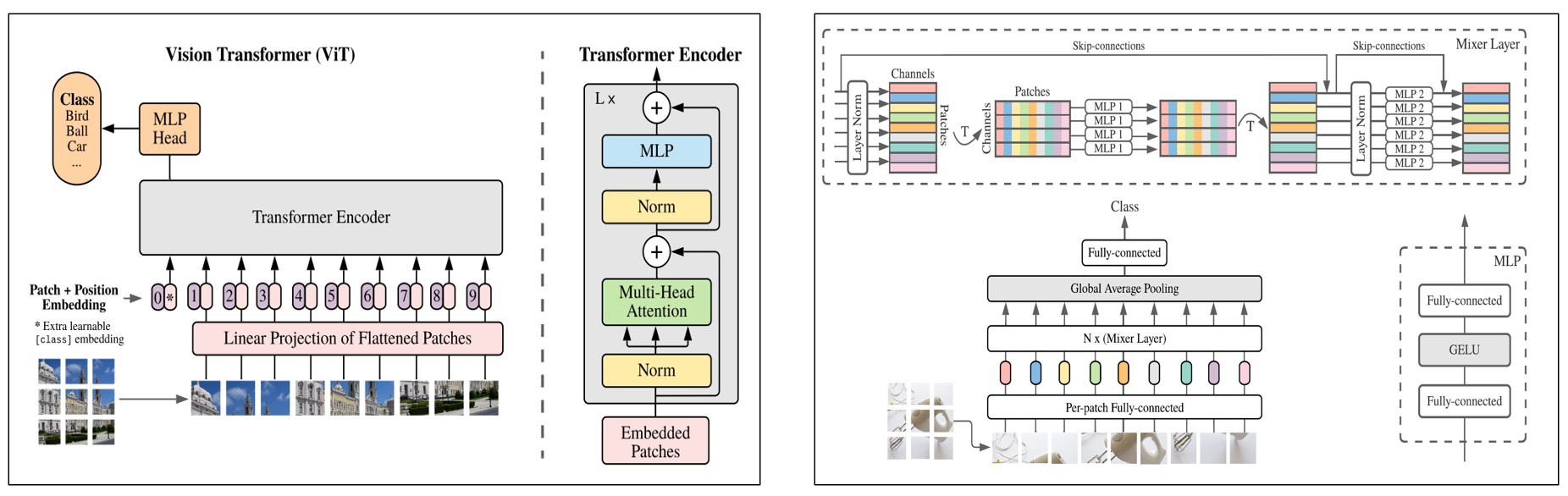
기존의 ViT(Vision Transformer)의 경우 Transformer architecture에서의 Encoder layer를 활용하여 이미지 분류 문제를 해결하였다. 본 논문에서는 "Attention mechanism"없이 오직 "Fully Connected Layer"만을 활용하여 이미지 분류 문제를 해결하였다.
두 구조의 가장 큰 차이점들은 다음과 같다.
1. Attention Mechansim 유무
2. Position Embedding 유무
3. Class Token의 유무
정도로 나눌 수 있다.
Abstract
- 최근, ViT와 같은 어텐션(Attention)기반의 네트워크들은 인기 있는 상태이다.
- 해당 논문에서는 저자들은 Convolution과 Attention 모두 중요하지만 둘 다 필요하지 않음을 보여준다.
- 저자들은 MLP-Mixer를 제안하는데 이는 Multi-layer Perceptrons(MLPs)으로만 구성되었다.
- MLP-Mixer는 이미지 분류 밴치마크와 경쟁적인 점수를 SOTA와 비교할 수 있는 성능을 얻었다.
Main Architecture of MLP-Mixer
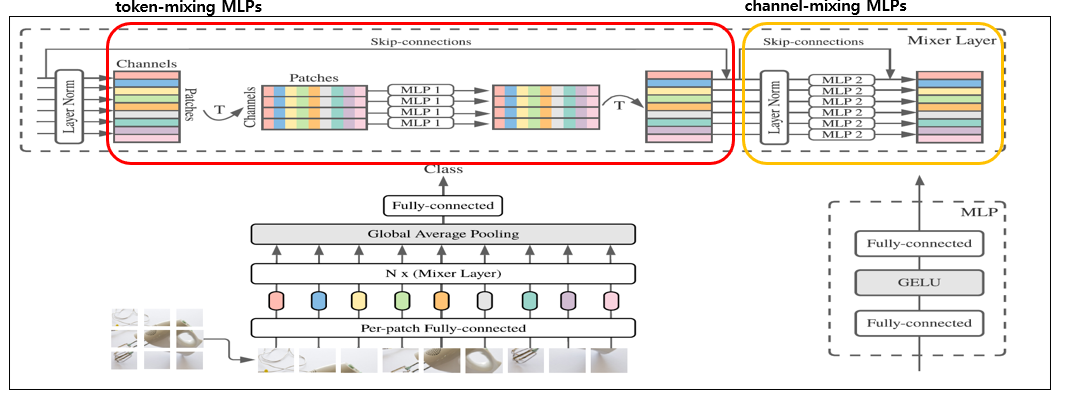
MLP-Mixer에 두가지 주요한 모듈이 존재한다.
1. Token-mixing MLPs
2. Channel-mixing MLPs
1,2는 각각 다른 토큰간의 MLPs와 각 토큰에 대한 MLPs로 구성되어있다.
Token-mixing MLPs에서 가장 주요한 점은 다른 토큰(patch)간의 MLPs를 통해 전역적인 정보를 받아드리는 점이 존재하고
Channel-mixing MLPs에서는 단일 토큰(patch)에 대해서 지역적 정보에 대해서 MLPs를 수행한다는 점이다. 이를 다르게 생각하면 Patch전체에 대한 NXN Convolution layer를 적용한 것과 동일하다. 하지만 차원을 $1 \times V_{C}$으로 평평한(flatten)상태이기 때문에, $C_out \times C_in \times 1 \times 1$의 Convolution layer와 동일한 Linear Layer로 동작하게 된다. 결국 Convolution layer가 하는 역할을 Fully Connected Layer가 '대체'한 것과 동일한 상황인 것이다.
이와 마찬가지로 Token-mixing MLPs 또한 Convolution layer로 처리가 모두 가능하다. 보다 자세한 것은 뒤에서 언급하겠다.
Each Module
1. Pre-patch Fully-Connected Layer

위의 그림은 "Pre-patch Fully-connected Layer"를 시각화 한 것이다.
아래는 위 과정의 순서이다.
1. NXN 크기의 Patch로 이미지를 나눈다.
2. NXN 크기의 Patch들을 Flatten한 후, Pre-patch Fully Connected Layer의 입력으로 넣는다.
3. 각각의 Patch에 대한 Vector들을 생성한 하여 이를 Token-mixing layer의 입력 값으로 활용한다.
여기서 위의 과정을 $V_{D_{S}} \times C_in \times N \times N$로 처리할 수 있다. => 따라서 Open source를 확인한다면 다음과 같이 Convolution layer로 위의 과정을 처리하는 소스가 다수 존재한다.
본 과정은 ViT의 과정과 동일하다. 또한 Patch의 크기와 수는 모델 성능에 대해 굉장히 직접적인 영향을 주기 때문에 실험적으로 여러 Patch 크기와 Patch 수에 대한 조사들이 존재한다.
또한 이러한 Patch로 나눠주는 작업을 통하여 Fully-connected layer를 하더라도 Convolution layer와 같은 지역적인 특징을 찾을 수 있는 점이 유지되는 강점이 존재한다.
=> 추후 타 연구들에서 Transformer architecture이 "Attention Mechanism"이 성능에 주요한 영향을 주는 것이 아닌 Patch로 나누는 작업 자체가 보다 더 중요하다는 논문들이 존재한다. 또한 본 논문에서도 가장 주요 기여가 "Attention Mechanism"을 하지 않고도 높은 성능을 얻는데 의미를 보여준다.
2. Token-mixing MLPs
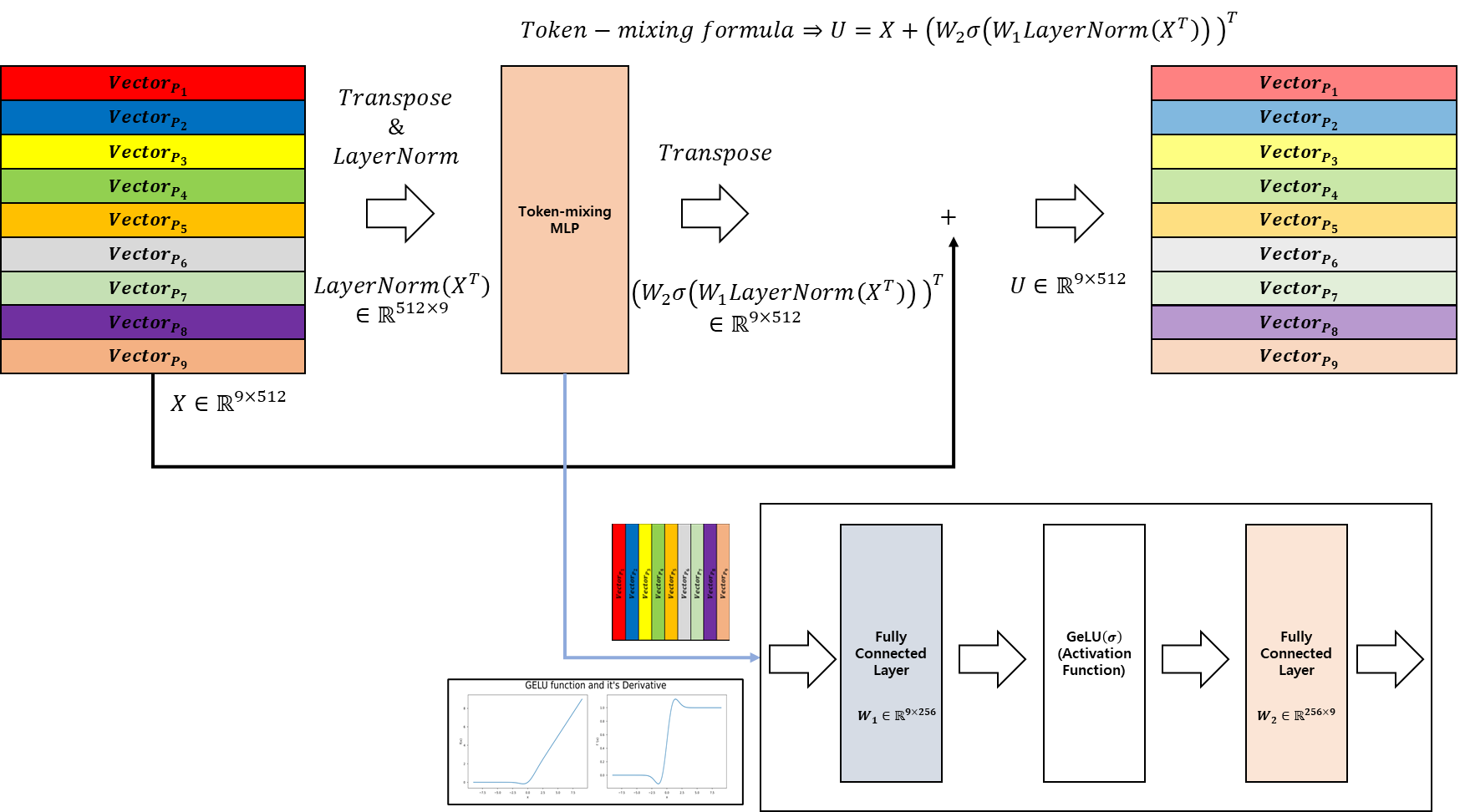
Token-mixing layer의 입력 값은 Pre-patch Fully-connected Layer의 출력값 또는 mixer layer의 반복 횟수가 1보다 클 경우에는 Channel-mixing layer의 출력값이 입력값으로 활용된다.
해당 Token-mixing layer에서 처리하는 연산은 Fully connected layer 두개와 Activation function(Gelu)한개로 구성되어 있으며, 입력 값이 Transpose된 값으로 들어간 후 Fully-connected layer 연산이 수행되기 때문에 각 Patch내에서의 Fully connected layer가 아닌, 동일한 spatial한 위치에 대해서 토큰(Patch)간의 Fully-connected 연산이 수행된다.
자세한 연산 과정은 아래에서 볼 수 있다.

위의 그림은 Token-mixing layer의 연산 과정이며 그림에서 위의 연산은 Fully-connected layer의 연산을 위해 Transpose 후 Fully-connected layer에 입력 값으로 활용된 후 출력값이 나오는 것을 보여주는 예시이며, 아래의 그림은 Transpose를 하지 않은 입력 값에 대해서 Convolution 연산을 통하여 동일한 역할을 하도록 수행한 결과이다. 이를 통하여 Token간에 대해서 Fully-connected layer 연산을 통하여 토큰간의 연관성을 학습을 하게 된다. CNN관점에서 볼 경우에 굉장히 큰 Receptive Field로 구성된 Conv layer(하지만 deliation을 활용하여 중간의 padding이 굉장히 큰 CNN)로 연산을 하는 것과 동일한 효과를 낼 수 있다. 이를 통하여 단순 CNN만을 활용하여 모델을 구성했을때에 비해서 전역적인 정보를 얻을 수 있는 강점이 존재한다.
3. Channel-mixing layer
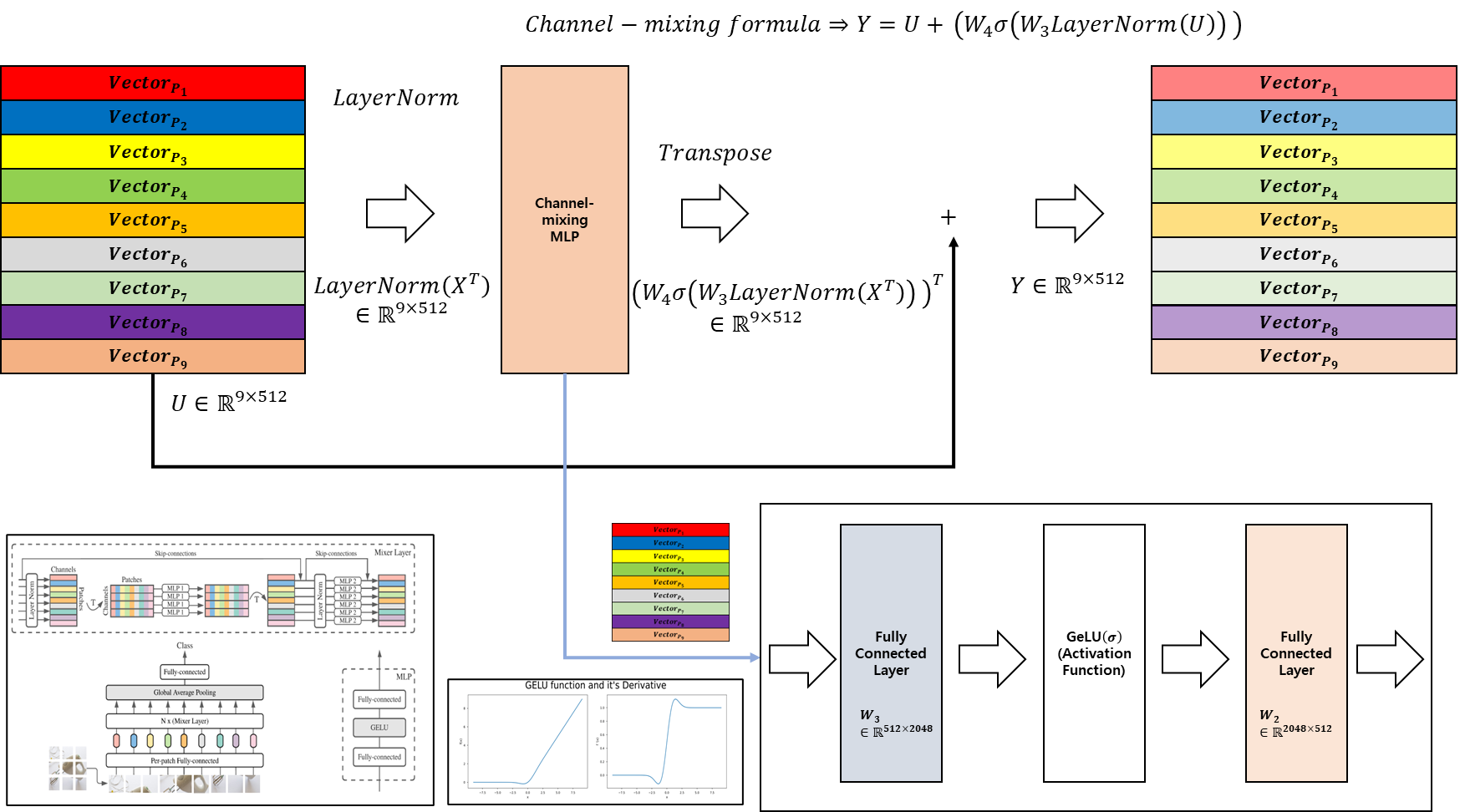
위의 그림은 Channel-mixing layer의 구조이다. MLPs의 구성은 Token-mixing layer와 동일하지만 다른점은
1. 차원의 크기가 다르다(아래의 Table에서 추후 언급하도록 하겠습니다.)
2. 입력 값의 형태가 Transpose가 되지 않은 상태로 입력으로 들어가게 된다.(해당 부분 때문에 Token-mixing layer과 다른 점이 존재합니다. (Fully-connected layer 연산의 방향이 다름.))
이를 통하여 각 패치별로 독립적으로 Fully-connected layer를 연산하기 때문에 "Channel-mixing layer"이라고 표현합니다.
따라서 토큰간의 연산은 존재하지 않고 토큰별로 독립적으로 연산이 수행됩니다. 이는 Patch크기로 잘랐기에 NXN convolutional layer와 유사한 형식으로 처리가 될 수 있지만 이전 "Token-mixing layer"에서의 전역적인 정보를 얻었기 때문에 완벽한 local적인 특징만을 가진다고는 할 수 없습니다. 하지만 이는 CNN에서도 동일한 역할을 가지기 때문에 큰 문제는 되지 않습니다. 오히려 단순 CNN 구조보다 지역적인 특징을 보다 잘 보존할 수 있는점을 가질 수 있습니다.(CNN구조의 경우 깊게 쌓기 위해서 Receptive field를 작게하기 위하여 3X3 convolutional layer filter를 사용하게 되는데 이를 반복적으로 쌓다보면 receptive field가 넓어지게 된다. 따라서 ResNet-18의 경우 최종 출력의 값의 표현 범위가 입력 크기에서의 32X32 크기정도를 담당한다고 하지만, CNN연산의 특성상 32X32보다 넓은 범위의 영역에 대해서 접근할 수 있기 때문에 더 넓은 영역의 정보를 가진다고 할 수 있다. 하지만 Patch로 나눠서 Linear연산을 수행할 경우에는 지역적인 범위를 그 이상을 넘지 못하도록 강제적으로 제약을 걸 수 있기 때문에 보다 정확한 영역을 구분지을 수 있을 것이다. 하지만 이전 Token-mixing layer를 통해 지역적인 특징 외의 전역적인 특징을 보는 점에 있어서 완전히 보존된다고 볼 수 없다.)
Channel-mixing layer 또한 Token-mixing layer처럼 CNN처리를 할 수 있다. 이는 아래에서 볼 수 있다.
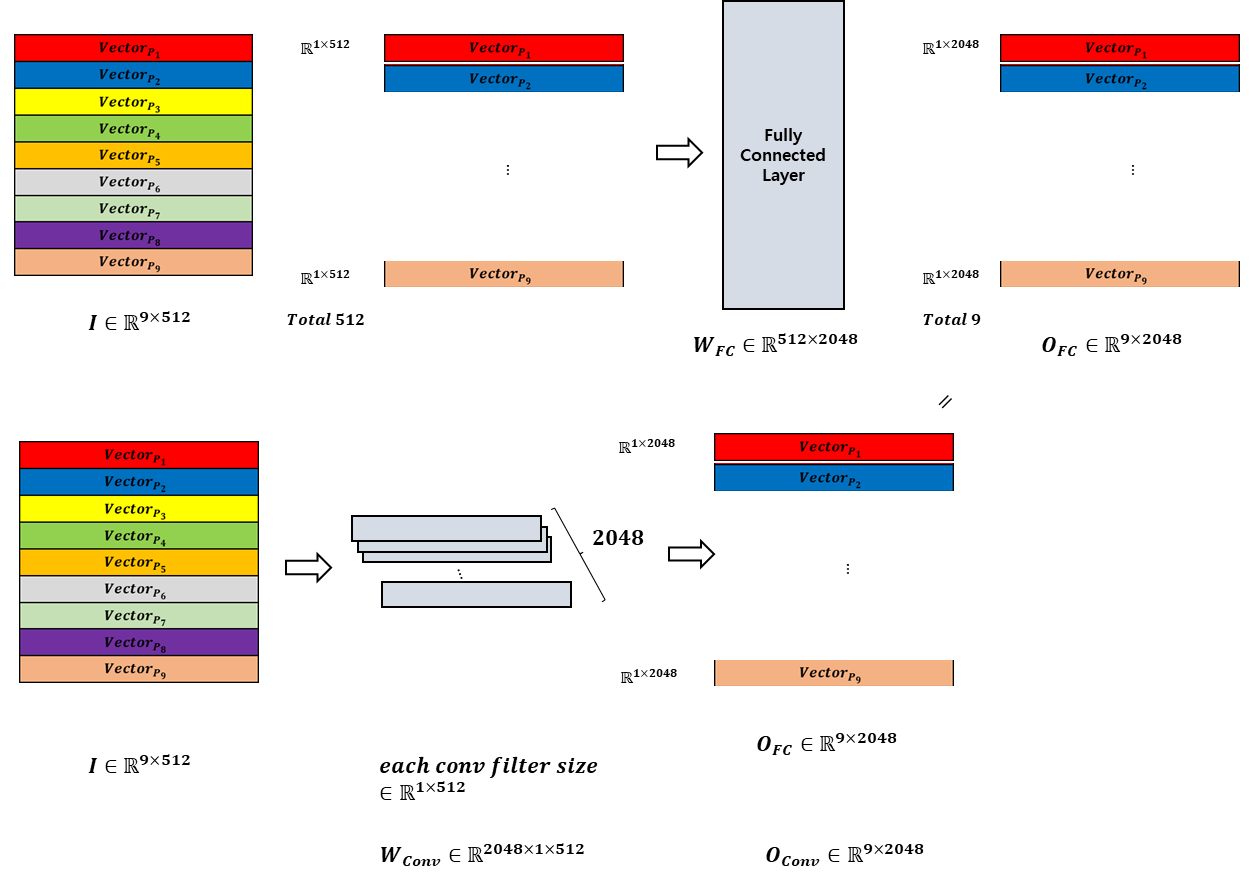
위와 마찬가지로 위의 경우가 Fully-connected로 연산하는 것이고, 아래의 경우가 CNN을 활용하여 연산을 하는 것이다. filter를 가로방향으로 처리할 경우 다음과 같이 동일한 연산을 수행할 수 있다. 따라서 큰 크기의 filter를 사용하여 처리하는 것이랑 동일하기 때문에 일반적인 CNN의 역할과 동일한 역할을 수행함을 알 수 있다.(대신 작은 필터로 여러번 쌓는 것이 아닌 각 patch에 대해서 한번에 처리한다는 점이 다른 점이다.)
Detail of Model Architecture
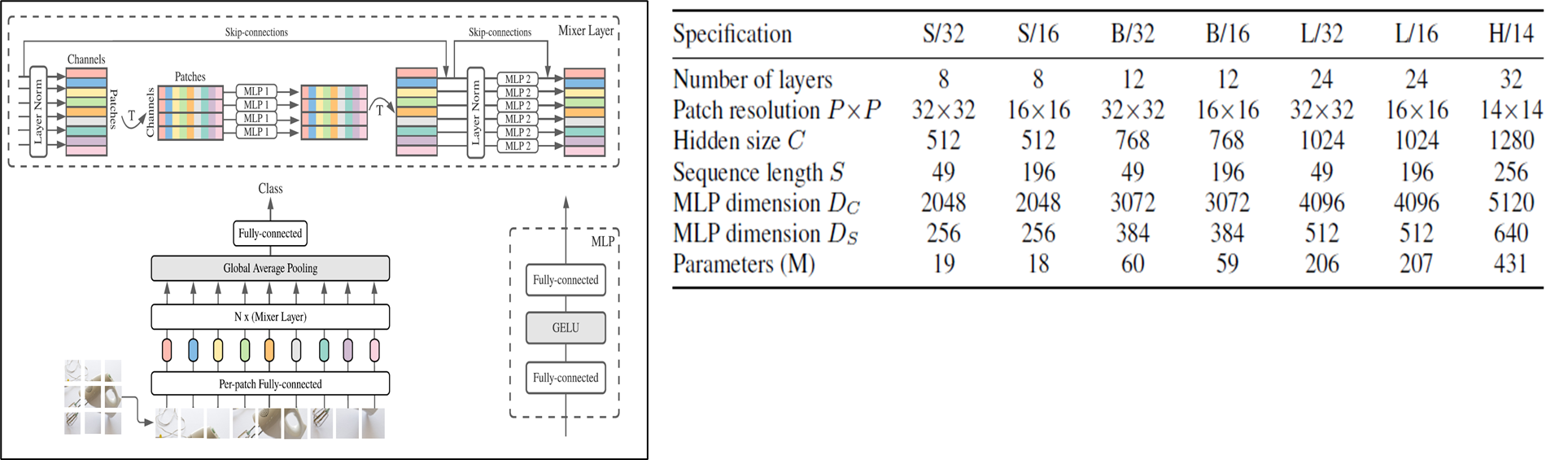
위의 표는 본 논문에서 제안한 방법에서 모델 구조의 상세 정보를 의미한다. 저자들은 모델의 크기별로 다음과 같이(S,B,L,H) 분류하였다.
알파벳(S,H,L,H) 옆의 숫자는 Patch의 해상도를 의미하며(크기) 아래의 P와 동일한 숫자이다.
Patch의 크기가 커질수록 동일 입력 해상도에서 적은 수의 Sequence length(S)가 생성이 된다. 같은 해상도에서 Patch의 크기가 클 경우 S의 수는 작아지고 패치의 크기가 작을수록 S의 크기가 커지는 것을 확인할 수 있다.
Number of layers는 Mixer Layer의 반복 횟수를 의미하게 된다.
$D_C$는 channel-mixing의 Fully connected layer의 차원을 의미하고, $D_S$는 Token-mixing에서의 Fully connected layer의 차원을 의미한다.
최종적으로 Parameters는 모델 학습 파라미터의 개수를 의미하는데 Patch의 수가 많다고 해서 Parameter의 수가 달라지지 않기 때문에 차이가 나타나지 않는다.(파라미터수는 동일하겠지만 연산이 되는 수는 S가 클수록 많아지게 된다.)
Results
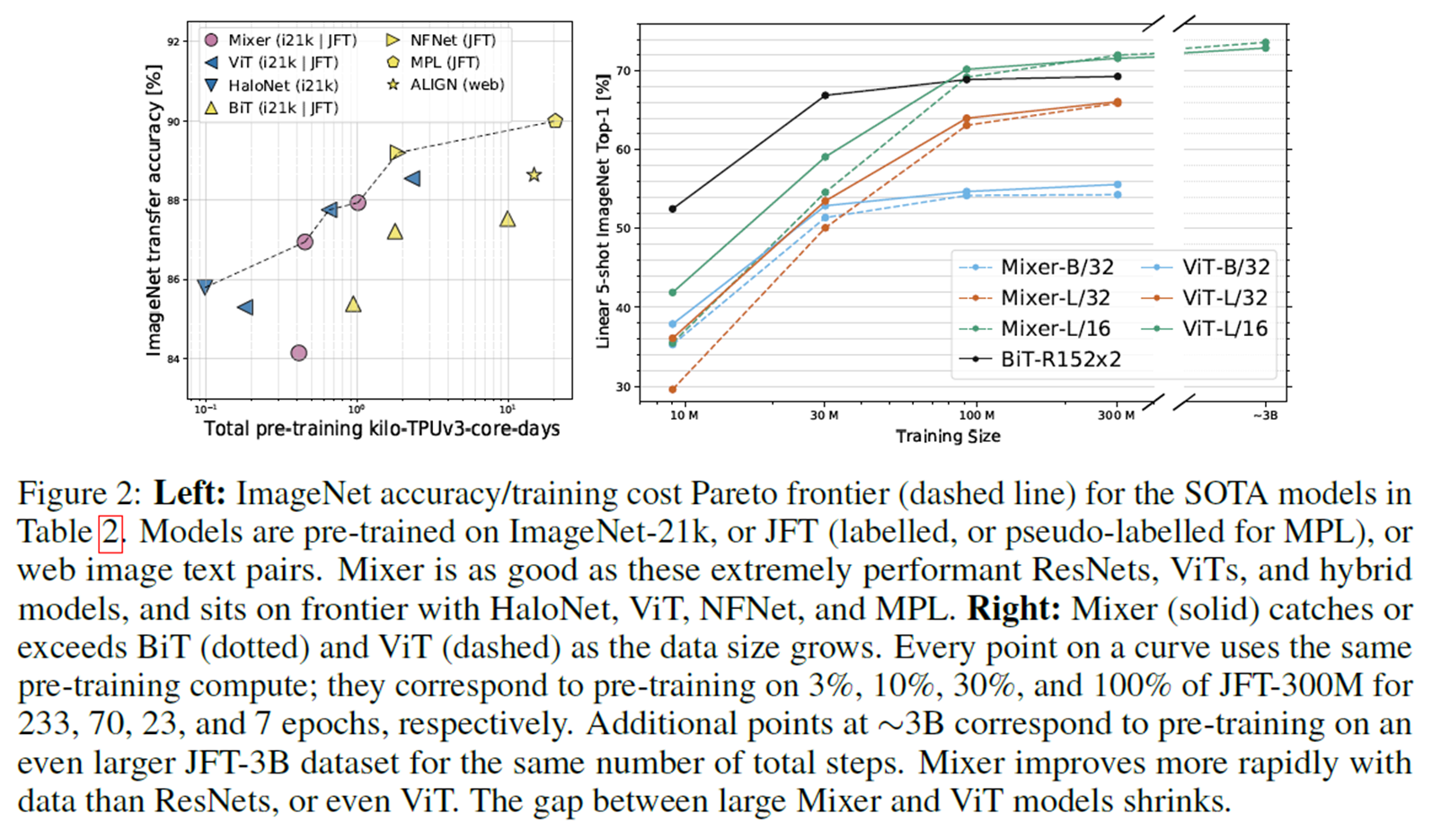
위의 그림이 보여주는 바는, 다른 SOTA architecture과 비교했을 때의 효율성을 보여주기 위한 그림이다.
Mixer(본 논문이 제안한 방법)은 다른 모델들에 비교해도 충분히 높은 성능을 얻음을 볼 수 있다.
좌측의 그림은 기존의 정확도-계산에 대한 trade off를 보여주며 이는 기존의 신경망 구조와 경쟁이 가능한 수준임을 강조한다.
우측 그림은 유사한 환경에서 ViT 모델과 Mixer가 유사한 성능을 달성하였음을 보여준다.
이는 "Attention Mechanism"을 활용하지 않고 달성한 유의미한 성능이라고 저자들은 강조한다.(또한 물론 CNN으로 모델 구조를 구현할 수 있지만, 본 논문에서의 강조점중 하나로는 CNN과 Attention이 아닌 오직 Fully-connected layer만으로 모델을 구성하고도 높은 성능을 얻을 수 있음을 강조한다.)
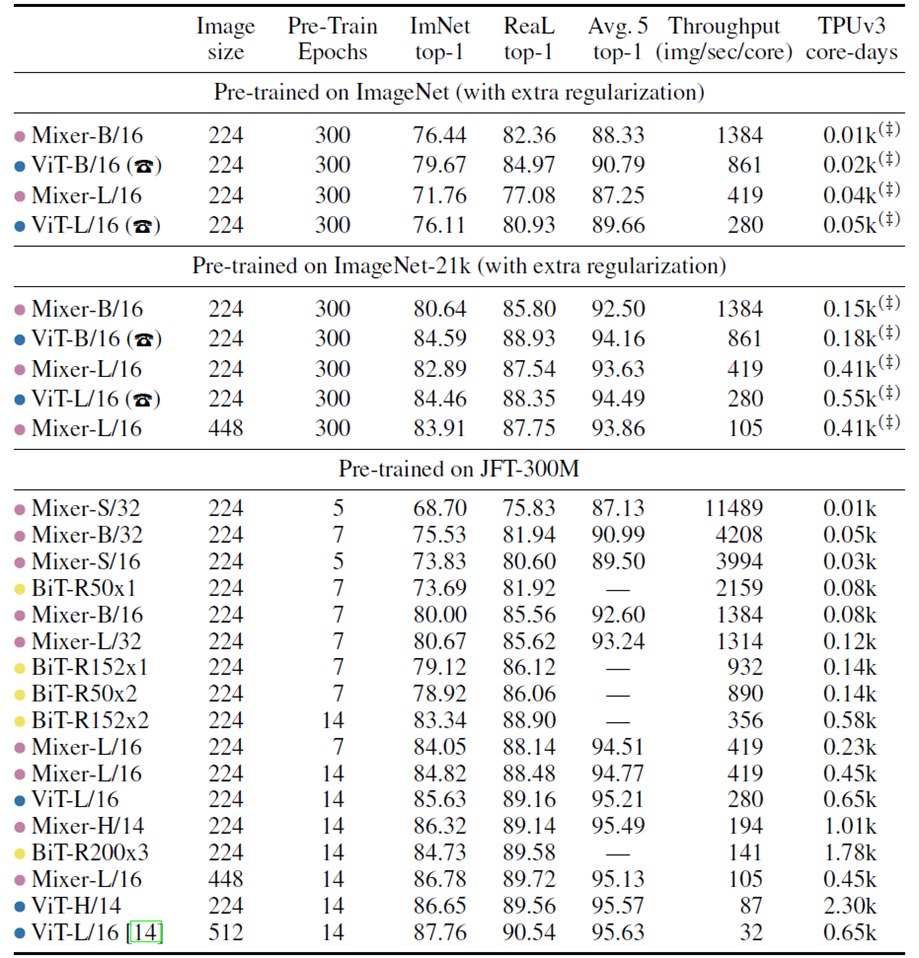
해당 테이블은 유사한 처리량의 모델과 비교했을 때, Mixer가 충분히 유의미한 성능을 얻음을 보여주기 위한 Table이다. 물론 성능 자체는 조금 떨어질 수 있지만 위에서 언급했듯이 오직 "Fully Connected Layer"만을 사용하고 얻을 결과이기에 충분히 유의미하다고 얘기할 수 있는 부분이다.
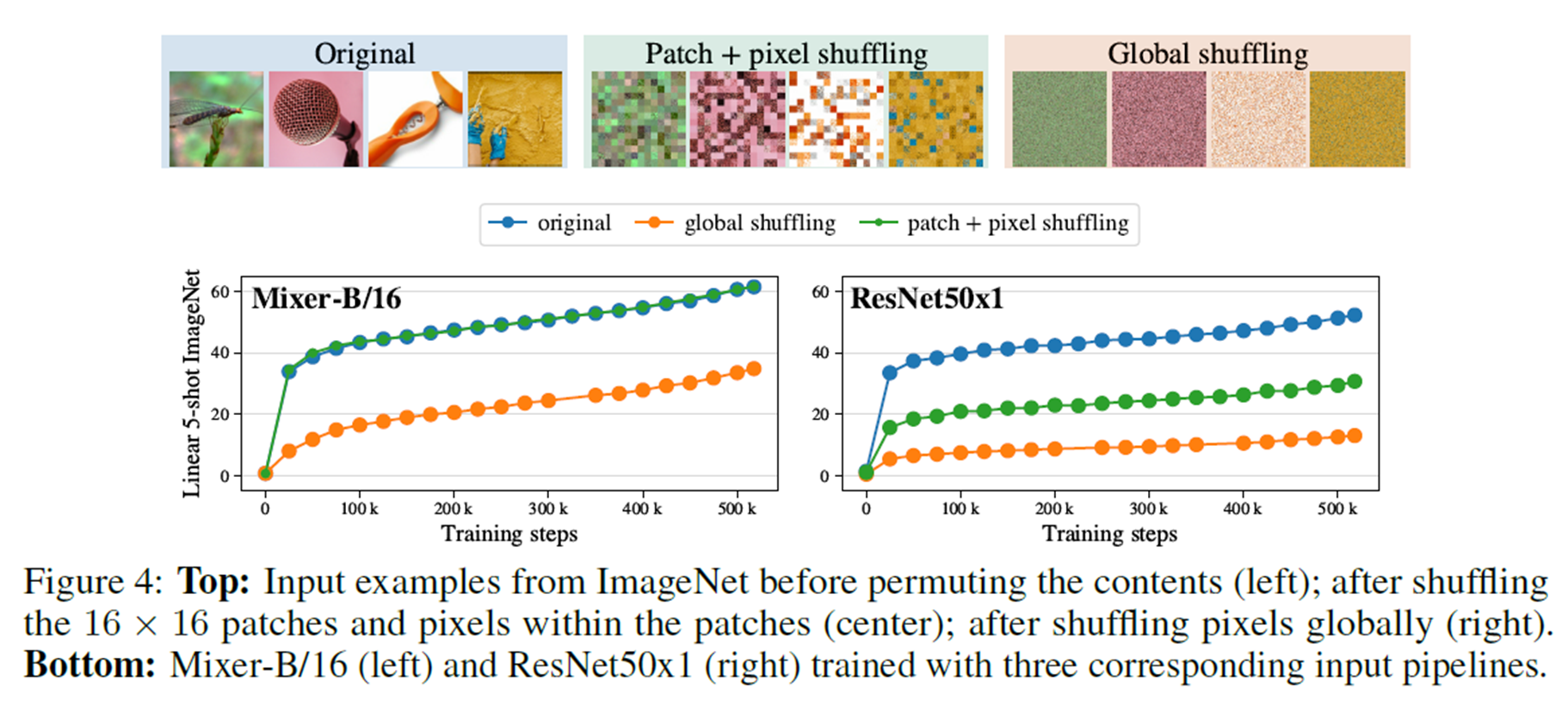
위의 그림은 굉장히 흥미로운 결과를 보여준다.
Original은 입력 이미지에 대해서 따로 처리를 하지 않은 것을 의미하며, Patch+pixel shuffling을 patch별로 shuffling을 수행한 것이다. 그리고 Global shuffling은 전체 이미지에 대해서 완전히 shuffling을 수행한 것이다. 따라서 Patch+pixel shuffling이 Global shuffling보다는 지역적인 정보가 유지된 것을 알 수 있다.
Mixer의 경우 3가지 경우에 대해서 나름 유의미한 성능을 얻음을 볼 수 있다. 특히 Patch-pixel shuffling을 수행하더라도 Original과 유사한 성능을 얻음을 볼 수 있으며 또한 Global shuffling에 대해서도 성능 감소가 이러나지만 상대적으로 적은 모습을 볼 수 있다.
ResNet50의 경우에는 두가지 경우에 대해서 큰 성능 감소가 있는 것을 볼 수 있는데, 상대적으로 Local 정보가 살아있는 Patch-pixel shuffling에 대해서는 성능감소가 덜 이뤄졌지만, Global shuffling의 경우 성능 자체가 나오지 않음을 볼 수 있다.
이를 통해 알 수 있는 것은 Mixer가 전역적인 특징을 활용하기도 하면서 Patch 내에서의 순서와 관련 없이 높은 성능을 얻을 수 있음을 볼 수 있다. 특히, Patch 내에서의 shuffling이 이루어 질 경우에는 Channel-mixing을 통해서 성능 유지가 가능한 것을 보여주는 것에 유의미하다. 또한 Global shuffling에서도 어느정도 견고함을 보여준다.

위의 그림은 Token-mixing layer의 값을 시각화 한 결과이다. 초기 Token-mixing layer의 경우에는 지역적으로 특징을 추출하다가 깊어질수록 전역적으로 정보를 반영함을 볼 수 있다.
결론(Conclusion)
- 저자들은 Vision에서 매우 간단한 구조를 제안했다.
- 저자들은 SOTA모델들과 비교했을때도 정확도와 학습과 추론에서의 연산 자원 필요량 사이의 trade-off를 통한 부분에 대해서 충분히 유의미한 것을 증명했다.