[논문정리] DeepSleepNet : A model for Automatic Sleep Stage Scoring Based on Raw Single-Channel 논문 리뷰

DeepSleepNet : A model for Automatic Sleep Stage Scoring Based on Raw Single-Channel

Akara Supratak, Hao Dong, Chao Wu, and Yike Guo

IEEE TRANSCATIONS ON NEURAL SYSTEMS AND REHABILITATION ENGINEERING, VOL. 25, NO 11, NOVEMBER 2017

---

Introduction

수면이란 사람 건강에 있어서 굉장히 중요학 역할을 한다. 그렇기에 의료 연구에 있어서 사람의 수면을 모니터링하는 것은 굉장히 유용하다.

사람의 수면 상태를 판단하기 위해서 사람의 몸에 센서를 부착하여 측정을 해야하며 전문가와 동반하여 진행된다.

이러한 센서들로부터 얻은 신호의 세트를 polysomnogram (PSG) 수면 다원 검사라고하며, electroencephalogram(EEG) 뇌파, electrooculogram (EOG) 눈의 움직임, electromyogram (EMG) 근전도 electrocardiogram (ECG) 심전도가 있다.

이러한 PSG는 30-s를 1 epoch으로 판단되며, 각 epoch마다 수면 전문가가 sleep stage (수면 상태)를 Rechtschaffen and Kales (R&K) 와 the American Academy of Sleep Madicine (AASM)에 의거하여 결정한다.

이러한 작업은 사람이 직접 진행하기 때문에 굉장히 시간 소요적인 작업이며 주관성이 들어가는 부분이 존재한다.

- 아무리 기준이 있다 하더라도 사람마다 해당 기준에 의해 결정하는 것이 모두 똑같지 않기 때문이다.

딥러닝 및 많은 분야에서 이러한 수면 상태를 판단하기 위한 노력들이 지속적으로 진행되고 있으며, 최근에는 딥러닝 분야를 통해 해결하고자 하는 부분들이 많이 생겼다.

해당 논문에서 소개하는 DeepSleepNet은 단일 채널 EEG를 기반으로 자동적 수면 상태 평가 모델이다.

보다 자세한 내용은 뒤에서 얘기하도록 하겠습니다.

---

그림 1. 위의 그림은 DeepSleepeNet의 모델 구조이다. Representation Learning 부분은 pre-training을 통해 우선적인 학습을 하는 CNN부분이며, Sequence Residual Learning에 해당하는 모델은 CNN부분을 통해 추출한 Feature값을 활용하여 Sequence 특성을 활용하여 보다 정확한 Sleep Stage Scoring을 하기 위한 방법으로 제시된다. 해당 구간은 RNN 계열인 bidirect-lstm을 활용하였으며 해당 lstm은 양방향 lstm으로 단방향 정보만을 사용하는 것이 아닌 양방향 정보를 사용할 수 있는 특징이 있다.

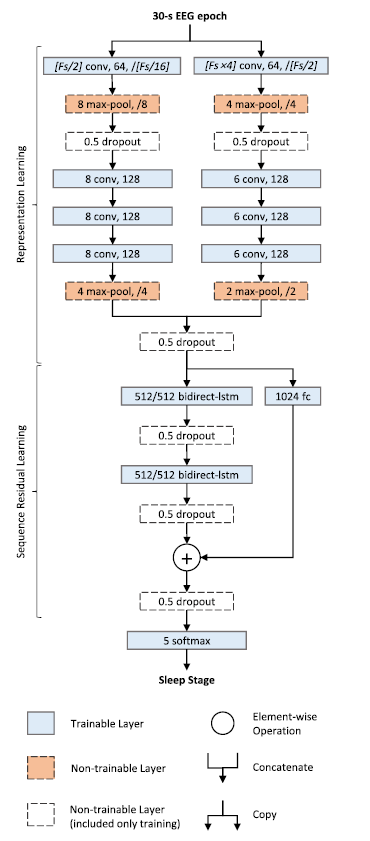
위의 그림 1.을 보면 DeepSleepNet의 모델 구조를 파악할 수 있다.

해당 모델의 구조는 Sample rate가 100Hz에 맞는 모델 구조이며, 실제 입력 값인 30-s EEG epoch는 $30(sec) {\times} 100 (Sample rate) = 3000$의 크기의 데이터가 들어가게 된다. 결과론적으로 1차원 convolution layer에 들어가는 구조는 $(1,3000)$ (1 = channel의 개수, 3000 = signal의 길이)이다.

해당 모델의 구조를 보면 알 수 있듯이 두개의 작고 큰 CNN구조로 branch를 나누어 진행이된 후 추후 concat을 통해 합쳐지는 작업을 하게 된다. 논문에서 말하기로는 작은 크기의 cnn의 시간적 특성을 추출하는데 특화되어 있으며, 큰 크기의 cnn의 경우 주파수 정보를 추출하는데 특화되어 있음을 말한다.

- 해당 부분에 대해서 생각하여 ResNet과 같은 일반적인 cnn모델에서 학습을 진행하였을 때, CNN부분만 사용하여 결과를 도출하였을 때 결과의 차이가 크게 존재하지 않았다. ( 실제 작은 cnn과 큰 cnn이 각각의 특성을 추출하는지에 대해서는 확신이 없다. )

추가적으로 과적합을 방지하기 위한 방법으로 Dropout을 사용한다.

그 외의 Maxpooling, convolution layer, lstm등 특별한 기술은 없다.

다만, lstm 같은 경우에는 hidden state를 저장하고 활용하는데 단방향이 아닌 양방향을 활용하기 위해서 bidirection-lstm을 사용하여 sequence에서 $t$의 경우 $t-1$과 $t+1$의 hidden state를 모두 활용할 수 있는 구조를 사용하였다.

- Sleep Stage를 결정하기 위해서 $t$를 기준으로 3~5개의 이전,이후 signals를 같이 보고 판단하기 때문에 해당 sequence 정보를 활용하기 위해 bidirection-lstm을 사용한 것으로 보인다.

모델에 대한 설명은 그림을 통해서 충분히 파악이 가능하기 때문에 넘기도록 하겠습니다.

그림 2. 해당 알고리즘은 학습 과정에 대한 정보이다. 4-8까지가 CNN부분을 사전 학습을 통해 추후 bidirection-lstm과 연결하였을 때 보다 높은 성능을 얻기 위한 작업이며, 모든 사전 학습이 끝난 후 fine-tuning과정으로써 미리 학습된 cnn의 weights를 활용하여 cnn은 weights 초기화를 진행하고 사전에 학습된 cnn부분의 파라미터의 업데이트를 위한 학습률(learning rate)는 작게 설정하여 기존에 학습을 통해 얻어진 weights에서 크게 벗어나지 않도록 설정하고, lstm의 학습률을 따로 설정하여 미세조정 작업을 진행하여 최종적인 모델 결과를 얻어낸다.

표 1. 각 데이터셋의 라벨 분포이다. N1의 수는 굉장히 적은 편이며, N2의 경우 굉장히 많은 비율을 가지고 있다.

여기서 중요한 점은 pre-training단계에서 표 1.을 보면 알 수 있듯이 클래스 불균형 현상이 존재한다. 따라서 이를 해결하기 위해 적은 수의 class의 signal을 복제하여 샘플의 수를 같게 맞춰주는 작업 ( oversampling )을 수행한다.

- 1차원 데이터의 경우에는 oversampling이 무조건적으로 좋은 결과를 초래하지 않기 때문에 보다 조심스럽게 한다고 말한다. 특히 jittering, rotation, cropping 등 많은 방법들이 존재하지만 보통 jittering정도를 사용하고 그 외의 방법은 지양한다.

CNN의 사전 학습이 종료가 되면 사전학습에 사용한 softmax를 없앤 후 bidirection-lstm과 연결하여 미세조정학습을 진행하게 된다. 자세한 방법은 그림 2.의 설명란에 자세히 적어두었다.

---

Regularization

정규화 방법으로 우선 dropout기법을 활용하였다. (학습 과정에서 랜덤한 노드를 0으로 만들어 학습을 하는 방법이다.)

dropout의 비율은 0.5로 설정하여 학습을 진행한다. ( 그림 1.을 보면 알 수 있다. )

두번째 방법으로 L2 weight decay를 활용하는 것이다.

loss function에서 단순 loss 값만 사용하여 학습하는 것이 아니라 추가적인 L2 weigh decay값을 더하여 loss에 반영하는 방법이다.

weight decay에서의 lambda는 $10^-3$으로 설정한다.

---

Results

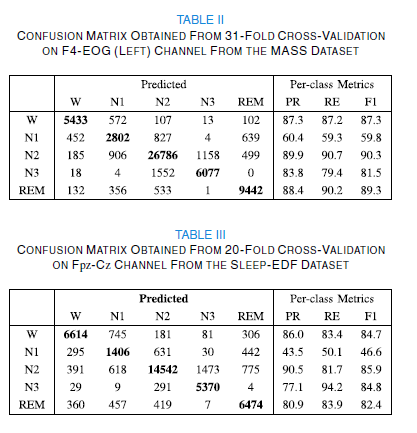
해당 논문은 Sleep-EDF와 Montreal Archive of Sleep Studies (MASS) 두개의 데이터셋의 결과를 활용한다.

- 해당 결과를 보면 따로 training set / Validation set / Test set을 구분짓고 학습을 하는 것이 아니다. 워낙 데이터의 수가 적다보니 ( sleep-edf 2013 의 경우 데이터의 수가 38개 이다. ) k-fold cross validation을 활용하여 학습을 진행하고 결과는 학습에 사용한 모든 데이터셋을 통해 결과를 보여준다. (결과에 들어간 데이터들이 결국 학습과정에서 학습에 사용된 데이터들이다. )

표 2. 표 3. 각각 데이터셋에 대해서 결과이다. 성능 평가 지표로 PR(precision) / RE(recall) / F1-score를 사용한다. 결과의 수를 보면 dataset의 비율과 같은 비율이다. ( 학습에 사용된 데이터로 결국 결과를 도출했다는 것 )

각각의 성능 지표의 수식은 아래와 같다.

$recall = \cfrac{TP}{TP+FN}$
$Precision = \cfrac{TP} {TP+FP}$
$F1-score = \cfrac{2}{recall^-1 + precision^-1} = \cfrac{2}{\cfrac{1}{recall} + \cfrac{1}{precision}} = \cfrac{2}{\cfrac{recall+precision}{recall{\times}precision}} = 2{\times}\cfrac{precision{\times}recall}{precision + recall} $

해당 논문을 구현하기 위한 소스에 대해서는 다음 포스팅을 통해 하도록 하겠습니다.