Be Your Own Teacher: Improve the Performance of Convolutional Neural Networks via Self Distilltation

Be Your Own Teacher: Improve the Performance of Convolutional Neural Networks via Self Distilltation

####Zhang, L., Song, J., Gao, A., Chen, J., Bao, C., & Ma, K. (2019). Be your own teacher: Improve the performance of convolutional neural networks via self distillation. In Proceedings of the IEEE/CVF International Conference on Computer Vision (pp. 3713-3722).

---

Abstract

본 논문에서는 self-distillation 학습 방법을 제안한다.

전통적인 Knowledge distillation인, 사전 학습된 teacher 네트워크의 출력을 softmax처리 한 값을 활용하는 방법과 다른 self-distillation은 모델 내부의 지식을 증류하는 방식을 활용한다.

---

Introduction

좌측 이미지 출처 : https://nervanasystems.github.io/distiller/knowledge_distillation.html 우측 이미지 : 본 논문 Figure 1. 지식 증류와 자가 증류의 학습 차이점에 대한 그림.

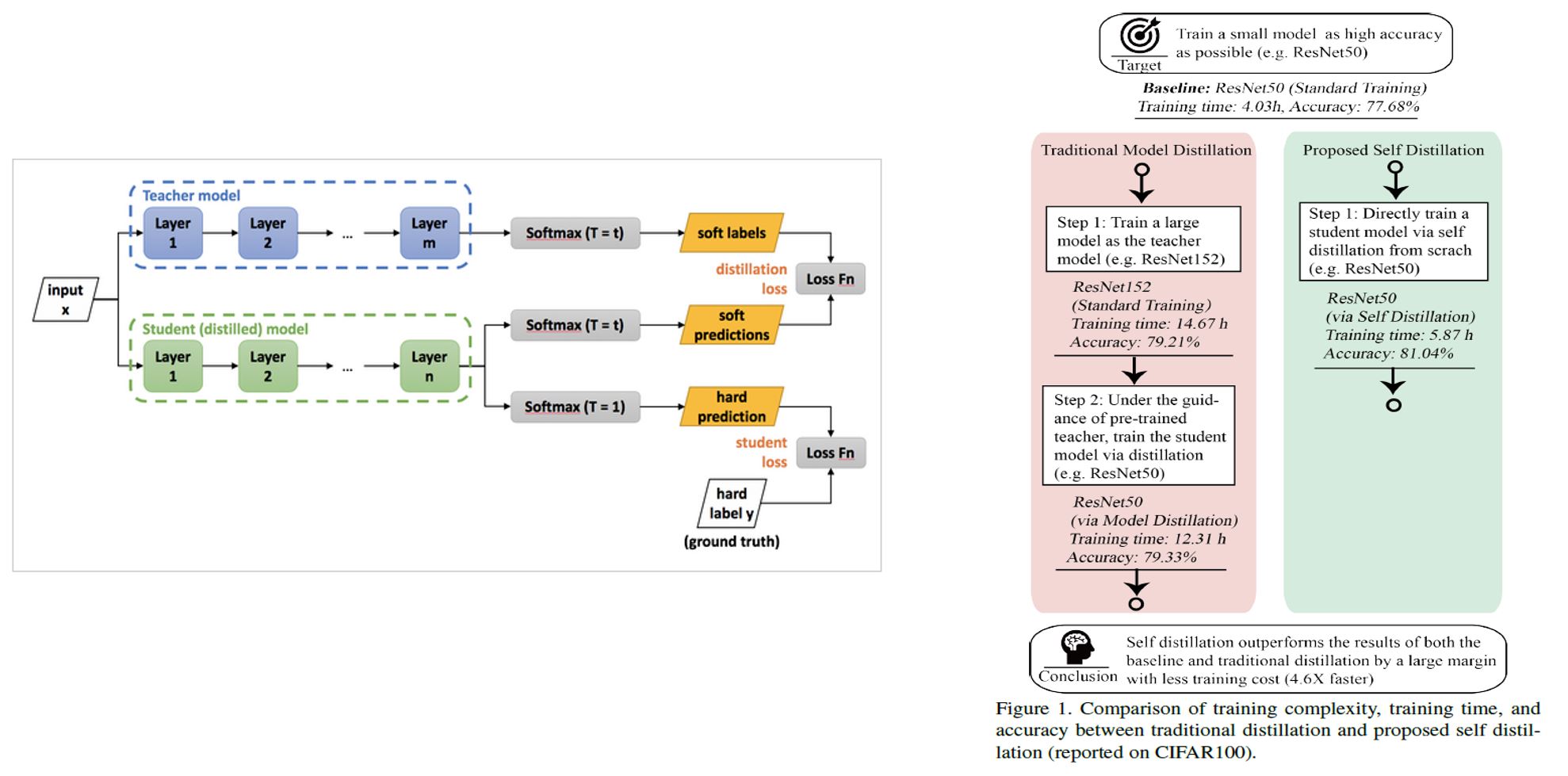
일반적인 지식 증류의 경우 왼쪽 그림과 같이 Student Model과 Teacher모델을 별개의 모델이다. (가중치가 다른 두 개의 모델)

따라서 일반적인 지식 증류는 two-step으로 학습이 이루어진다. first step으로 Teacher 모델을 사전 학습 한다. Second step은 사전 학습된 Teacher 모델과 Student 모델에 같은 입력 값을 통과 시킨 후 Student 모델의 업데이트에 활용되는 loss를 Cross Entropy와 KL Divergence Loss 두개를 활용하여 Student 모델을 학습시킨다.

Cross Entropy는 Student 모델의 Output과 Ground Truth label과의 loss function이다.

KL Divergence는 Student 모델의 Output과(Softmax) Teacher 모델의 Output(Softmax)간의 loss function이다.

$\alpha$ hyperparamter를 활용하여 두 loss function의 균형을 맞춘다. $\alpha$값이 높을 경우 Teacher 모델의 영향력을 높이는 것을 의미하며 반대로 낮아질 경우 Teacher 모델의 영향력을 줄이는 것을 의미한다.

자가 증류(Self-Distillation)의 경우에는 Knowledge Distillation과 다르게 One-step으로 학습이 이루어진다.

이는 증류를 단일 모델 내에서 진행하는 것을 의미한다.

Contribution

자가 증류는 ResNet과 VGG모델에서 성능을 향상시켰으며, 추가적인 응답 시간의 지출 없이 이루었다.

자가 증류는 다른 깊이에서의 classifier를 활용함으로써 정확도와 자원에 대해서 Trade-off를 수행할 수 있기 때문에 edge device에 대해서 적용하기 좋다.

실험을 통해 좋은 성능을 얻음을 보여주었다.

Methods

Self-Distillation모델 자세한 설명은 아래와 같다. 추가적으로 화살표가 softmax와 bottleneck block을 거쳐서 통과하는 것 처럼 보이지만 실질적으로 Final Layer의 softmax 출력과 Final Layer의 output Feature map과 바로 이어진다. 이는 Open Source를 통해 보면 이해하기 쉽다.

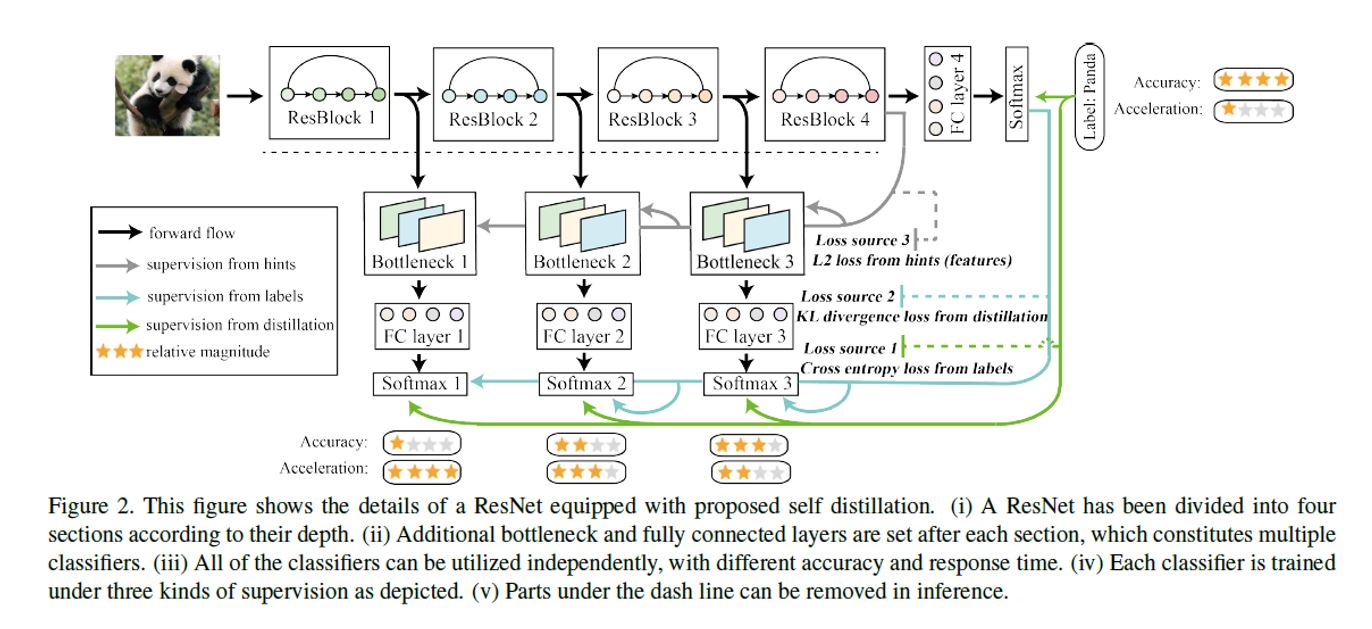
해당 학습 방법에서는 Loss가 총 3가지 방식의 Loss가 존재한다.

- Loss1 : $(1-\alpha) \times CrossEntropy(q^i,y)$

Ground Truth와 각 Layer의 Classifier간의 Cross Entropy Loss Function.

- Loss 2 : $\alpha \times KL(q^i,q^C)$

가장 깊은 Classifier의 예측값과 각 Layer의 Classifier(Softmax)간의 KL Divergence Loss Function

증류의 비율은 $\alpha$의 값에 영향을 받는다.

- Loss 3 : $\lambda \times |F_i - F_C|_2^2$

마지막 Layer의 Feature map과 이전 Conv Block Layer의 Feature map간의 L2 Loss Function

다음과 같은 방식을 활용하여 마지막 feature map에 맞도록 이전 Conv Block Layer의 feature map을 만들어지도록 학습시킨다.

최종 Loss Function

$$ loss = \sum_i^Closs_i = \sum_o^C((1-\alpha) \times CrossEntropy(q^i,y) + \alpha \times KL(q^i,q^C) + \lambda \times |F_i - F_C|_2^2) $$

---

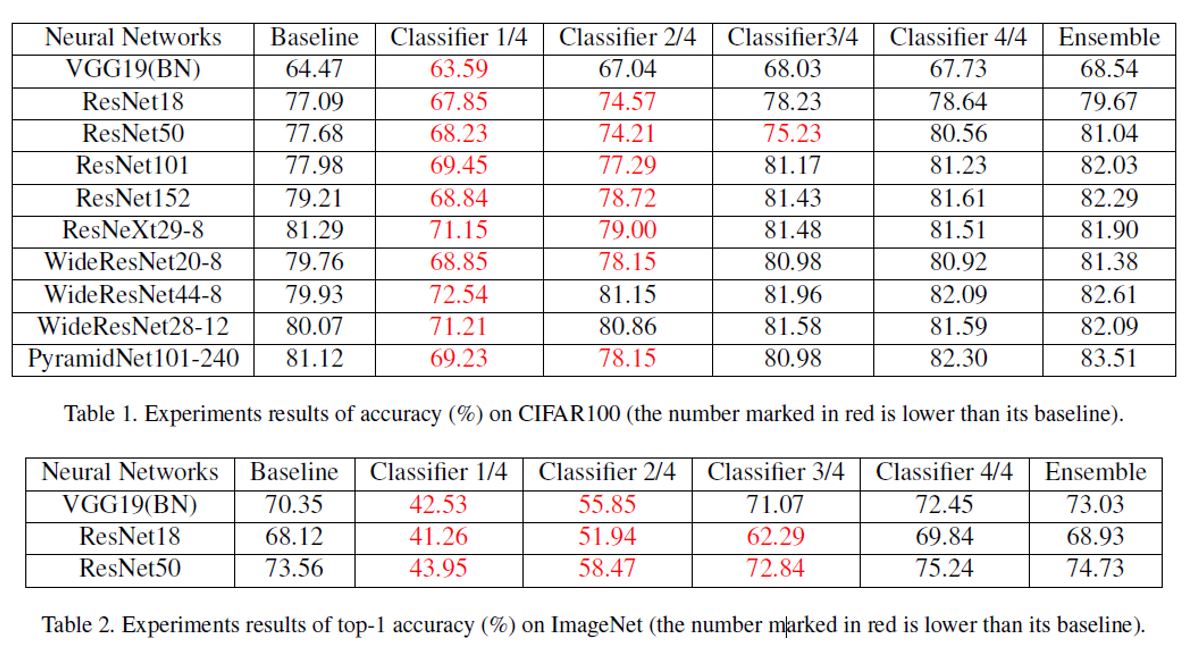
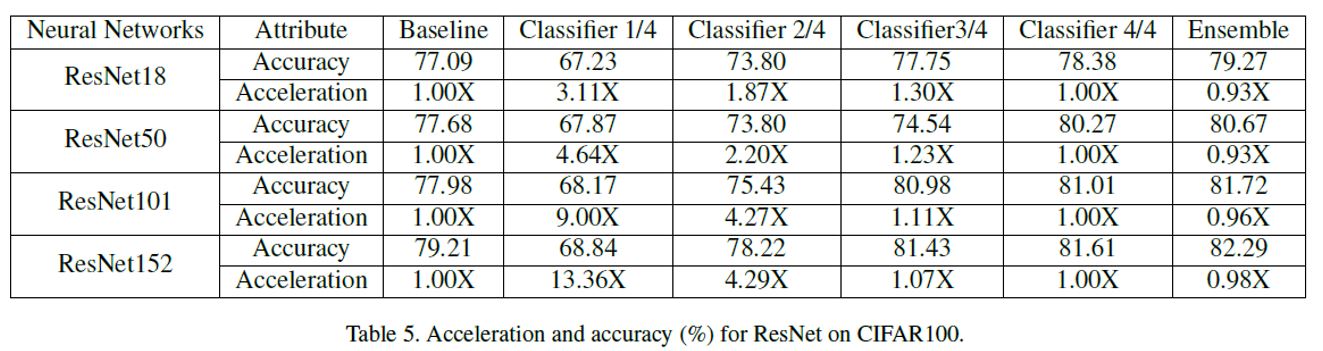
위의 Table들을 보면 알 수 있듯이 자가 증류를 활용할 경우 기본 Base Line보다 높은 성능을 얻을 수 있으며 만약 가속화를 하고 싶을 경우 좀더 낮은 깊이의 Classifier을 활용할 수 있는 선택을 가질 수 있다.

또한, 모든 Classifier에 대해서 Ensemble 처리를 했을 시 높은 성능을 얻음을 볼 수 있다. 일반적으로 Ensemble의 경우 높은 성능을 가지는 모델들을 조합하여 활용하는 방법을 사용하지만, 위와 같이 낮은 정확도를 가지는 Classifier에 대해서도 같이 Ensemble을 함에도 불구하고 높은 성능을 얻음을 볼 수 있다.

---

위의 그림들은 해당 방식의 강점에 대한 추가적인 설명이다.

1. 자가증류를 사용 유무에 따라 Noise에 대해서 강해지는 것을 Accuracy와 Loss의 값의 변화를 통해 보여주었다. 이는 해당 방식이 모델을 보다 견고하게 만든다는 것을 의미한다.

2. 자가증류는 Gradient Vanishing Problem을 보호해주는 것을 2번째 그림을 통해 보여준다. 특히 ResBlock 첫번째의 경우 Average Gradients가 자가증류를 썻을때 안썼을때보다 눈에 띄게 높은것을 볼 수 있다.

3. 깊은 층에서 보다 좋은 특징을 추출할 수 있음을 PCA를 통해서 보여준다. Classifier4로 갈수록 군집화가 더 잘 일어나는 것을 확인할 수 있다. 이는 단순 자가 증류에서만 일어나는 문제는 아니지만 낮은 깊이에서도 충분히 좋은 군집화가 일어나는 것을 보여줌으로써 자가증류를 통해 학습시 기존 모델보다 얕은 레이어의 Classifier를 활용하더라도 높은 성능을 얻음을 보여주는 근거가 될 수 있다.

---

ConClusion

본 논문에서 제안하는 자가증류와 이전 증류 방식을 비교하였다.

해당 기술은 속도와 정확도의 Trade off를 통해 조절을 제공하며 이전 증류의 필요성인 외부 teacher model이 필요가 없다.

flat minima, gradients 그리고 discriminating feature에 강함을 보여준다.

자가 증류는 가속화 모델 또는 압축 방법보다 모델의 성능을 보다 가속화 시킬 수 있다.