M2m : Imbalanced Classification via Major-to-minor Translation
2021. 5. 2. 17:57ㆍPapers/Data imbalance
M2m : Imbalanced Classification via Major-to-minor Translation
Kim, J., Jeong, J., & Shin, J. (2020). M2m: Imbalanced classification via major-to-minor translation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (pp. 13896-13905).
Abstract
실제 환경에서의 정답이 있는 학습 데이터셋은 일반적으로 굉장히 불균형적이지만, 실제 해당 데이터를 학습하는 모델을 균형적인 테스트 평가 기준을 만족해야 된다.
해당 논문에서는, 많이 등장하는(more-frequent classes) 클래스 샘플들을 변환을 통하여 덜 등장하는(less-frequent)클래스를 증대시킴으로써 해당 문제를 해결한다.
이 간단한 방법을 통해 classifier는 Majority information의 다양성을 전달하고 활용하여 Minority classes를 보다 일반화 가능한 features을 학습 할 수 있다.
경험상, 기존에 존재하는 re-sampling 또는 re-weighting 방식들보다 높은 성능을 얻음을 볼 수 있다.
Introduction
클래스-불균형 데이터셋은 일반적으로 모델을 일반화하는데 어렵게 만드는데, 특히 클래스 불균형 데이터셋으로 학습 후 균형 데이터셋에서 평가를 할 시 성능을 낮게 얻을 수 밖에 없다.
이러한 문제들을 해결하기 위해서 클래스간의 샘플 크기 측면에서 수를 조정함으로써 해당 문제를 해결하고자 하는 방법들이 제안되었다.
대표적으로 두가지 방법이 존재한다.
- Re-weighting : 클래스의 빈도에 따른 loss function에 weight값을 부여하여 문제를 해결하는 방식 ( weighted loss function )
- Re-sampling : 데이터의 분포를 변환하는 방식, ex) Over-sampling(minority classes), Under-sampling(majority classes)
하지만, re-balancing방식들은 흔히 minority classes에 대해서 over-fitting을 발생시키며, 이는 minority information의 부족에 의해 발생한다.
Over-sampling방식에서 SMOTE와 같은 방식이 존재하는데, 해당 방식의 가장 큰 문제는 minority 클래스의 수가 매우 적을 경우 굉장히 성능이 낮게 나타나는 현상이 발생한다. ( 따라서 Long-Tail dataset에 대해서 낮은 성능을 보여준다.)
- minority class에 대해서 over-sampling을 하기 위해, 가지고 있는 minority class를 활용해야 하는데, 활용해야 할 데이터가 적을 경우 결과론적으로 특징의 차이가 없는 데이터들로만 생성할 수 있기 때문에 크게 도움이 되지 않는다. ( 본 논문의 방식은 minority class를 oversampling하기 위해 minority class를 쓰는 것이 아닌 majority class를 활용하기 때문에 위의 문제점을 해결할 수 있다. )
Contribution
Majority 샘플은 인조 minority 샘플로 변환될 수 있으며 그것을 활용하여 최적화를 진행할 수 있다. 해당 데이터로 학습시킬 경우 majority class에 영향을 주지 않는다.
우리는 더 majority 클래스에서 생성하는(minority) 것이 더 바람직하다는 관찰을 기반으로 샘플 거부 기준(sample rejection criterion)을 설계한다.
제안 된 거부 기준을 기반으로 생성 과정에서(Over-sampling) 변형 될 다수의 시드를 샘플링하기위한 최적의 분포를 제안합니다.
Major-to-minor translation
$$x^* = argmin_{x:=x_0+\delta}{L(g;x,k)+\lambda\bullet f_{k_0}(x)}$$
$L$ : cross entropy
$\lambda > 0$ : hyperparameter
model $g$ 는 long-tail dataset에 대해서 사전 학습된 모델(pre-trained) (가중치가 고정되어 있음)
model $f$ 는 M2m 학습 방법을 적용하여 학습시킬 모델(학습하는 모델)
$x^*$ : 새롭게 만들(인조) over-sampling 데이터
$x_0$ : x(minority class)에 비해 상대적으로 majority class
$\lambda$ : 해당 값에 따라 새로 학습시킬 모델 $f$의 반영의 유무를 결정할 수 있다. 해당 값이 너무 클 경우 $f$모델에 너무 적합한 결과를 초래할 수 있다.(over-fitting)

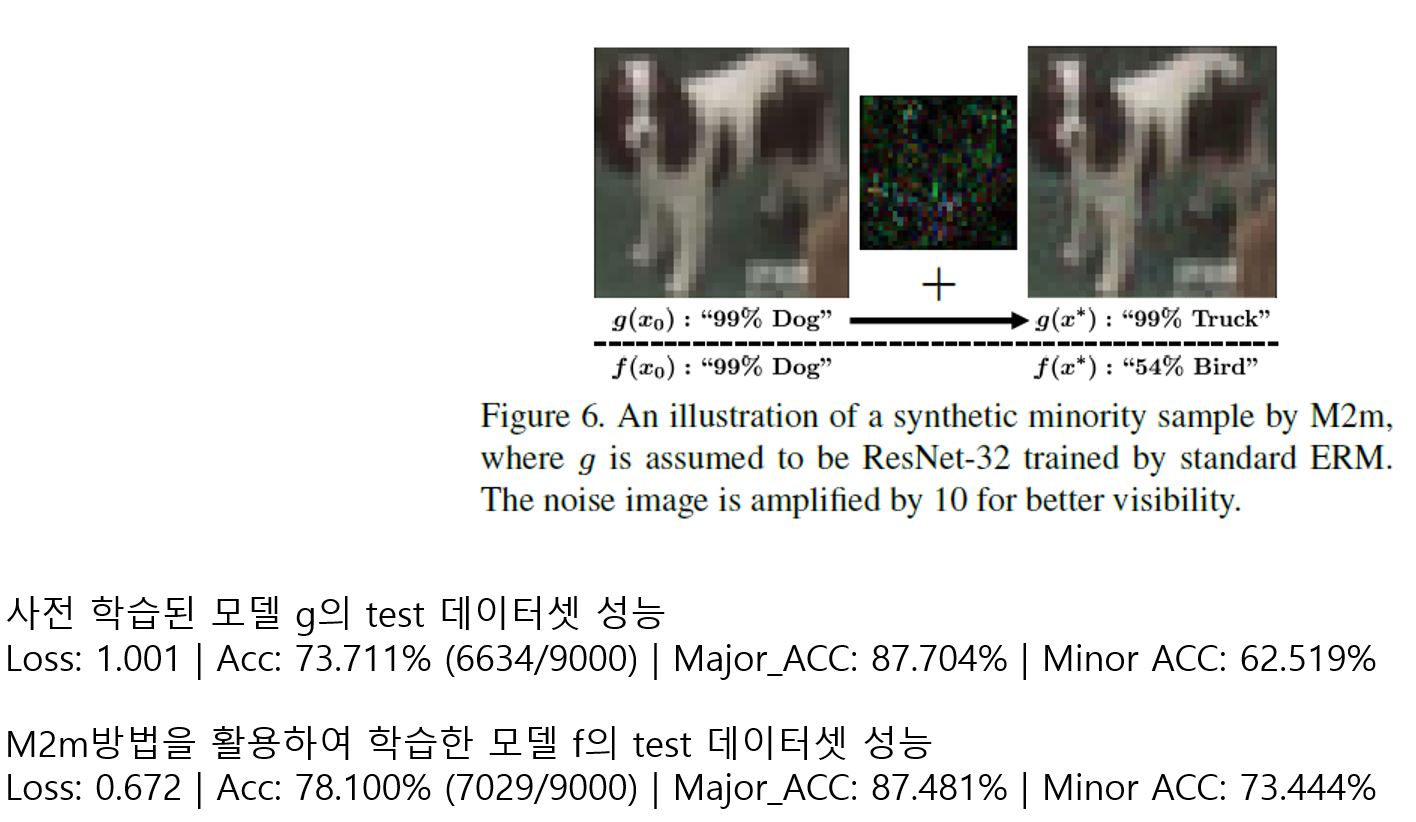
해당 방식을 보면 알 수 있듯이 일반적으로 모델이 학습 데이터에 대해서 기울기를 구한 후 해당 기울기 값을 활용하여 모델의 가중치를 업데이트하는데, 반대로 모델을 학습하는 것이 아닌 이미지를 minority class에 위치할 수 있도록(특징) 변화시켜주는 작업을 하는 것이 바로 M2m 방식이다. 만약 $T = 5$일 경우 위의 그림과 같이 5번의 변화를 통해서 기존 $x_0$가 $x^*$으로 변화하는 것을 표현할 수 있다.
여기서 또한 $\lambda == 0$일 경우 f의 영향력이 사라지기 때문에 위의 그림처럼 파란색 구역으로 가지 못하고 빨간색 영역에서 움직이는 상황이 발생할 수 있다. 따라서 적당한 $\lambda$값을 설정해주는 것이 중요하다.
M2m Over-sampling Algorithm




Result

위의 표와 같이 M2m의 성능이 높은 것을 볼 수 있음.